Des centaines d'exercices de DS

Fonctions Suites Géométrie Vecteurs Pourcentages Dérivées Expo LN Intégrales Complexes

Essaie les exercices de DS, clique ci-dessous

Choisis ton exercice de DS !

Maths de première : exercice pour trouver les coefficients d’un polynôme du troisième degré. Courbe, dérivation, équations, système.

Exercice N°797 :

Exercice, trouver coefficients polynôme, dérivée, équation, première

Exercice N°797 :

Afin d’éviter le passage en centre-ville d’une ligne TGV, on effectue un changement du tracé de cette ligne. Sur le plan ci-dessous, G
représente l’ancienne gare et C la nouvelle gare desservant la ville.

Trouver coefficients polynôme, dérivée, équation, première, schéma

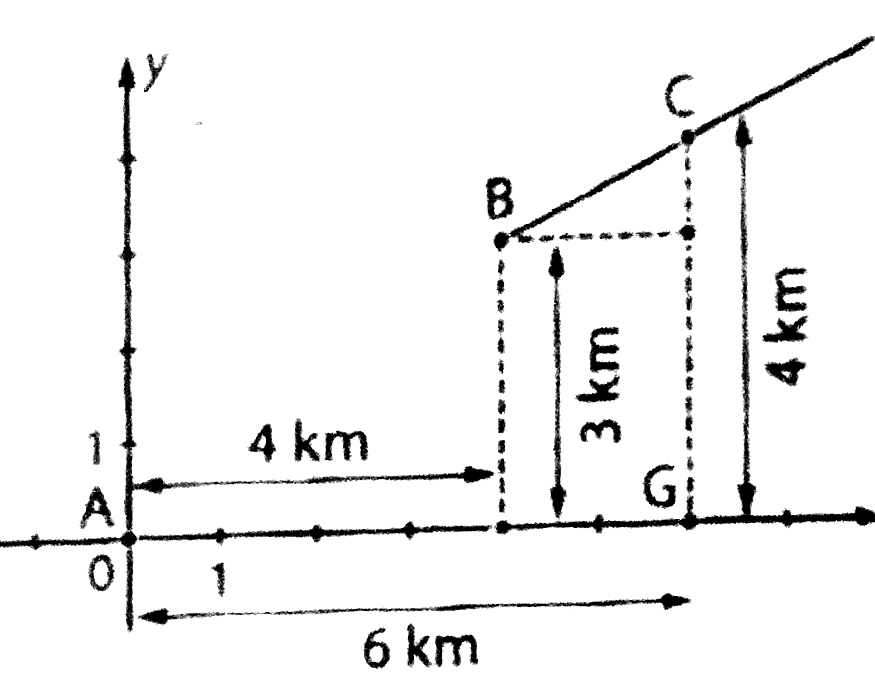
On se propose de raccorder des deux tronçons rectilignes, c’est-à-dire la partie de l’axe des abscisses à gauche de A et la demi-droite [BC], par une courbe plane.
Le raccordement doit être tangent à ces deux tronçons rectilignes.

On modélise le problème du traçé à l’aide d’une fonction f définie sur R de la forme :
f(x) = ax3 + bx2 + cx + d
avec a, b, c et d quatre coefficients réels.

Le raccordement se fait entre les points A et B. On choisit un repère d’origine A comme c’est indiqué sur le schéma. L’axe des abscisses est la droite (AG).

1) Justifier que f(0) = 0 et que f ‘(0) = 0. Lis la suite »

Ecris le premier commentaire

Maths de première : exercice d’optimisation de surface d’un triangle avec dérivation, tableau de variation, polynôme, racine carrée.

Exercice N°796 :

Exercice, optimisation, surface, triangle, variation, première

Exercice N°796 :

Soit la fonction f définie sur R par :
f(x) = -x4 + 400x2.

1) Montrer que la fonction f est dérivable sur R et déterminer sa dérivée f ‘(x). Lis la suite »

Ecris le premier commentaire

Maths de première : exercice d’optimisation de l’aire d’un triangle avec dérivation, tableaux de signe et de variation, trouver le maximum.

Exercice N°795 :

Exercice, optimisation, aire, triangle, tableau de variation, première

Exercice N°795 :

Dans un repère orthonormé du plan, on considère la parabole P d’équation
y = -(2/9)x2 + 8.
La parabole est représentée graphiquement sur le schéma ci-dessous :

Optimisation, aire, triangle, tableau de variation, première, schéma

La parabole coupe l’axe des abscisses en les points A(-6 ; 0) et B(6 ; 0). Soit un point M sur l’arc de parabole compris entre les points A et B et H son projeté orthogonale sur le segment [AB].

On considère la fonction f définie sur l’intervalle [-6 ; 6] par l’expression :
f(x) = -(1/9)x3 – -(2/3)x2 + 4x + 24.

1) Montrer que l’aire du triangle AMH est égale à l’expression f(x). Lis la suite »

Ecris le premier commentaire

Maths de première : exercice d’optimisation du volume d’une boîte. Hauteur, dérivation, tableau de signe, tableau de variation, maximum.

Exercice N°794 :

Exercice, optimisation, volume, boîte, hauteur, dérivation, première

Exercice N°794 :

On entoure une boîte avec un ruban de longueur totale 1.20 m dont 20 cm ont permis de réaliser le noeud. La boîte est un pavé droit à base carrée et le ruban passe par le milieu des arêtes des faces supérieures et inférieures, comme c’est indiqué sur le schéma ci-dessous.
On désigne par x la longueur du côté du carré (en mètre) et on désigne par h la hauteur de la boîte (en mètre).

Optimisation, volume, boîte, hauteur, dérivation, première, schéma

1) Montrer que l’on a l’égalité :
4x + 4h = 1. Lis la suite »

Ecris le premier commentaire

Maths : exercice de trigonométrie avec équations de première. Sinus, cosinus, second degré, intervalles, angles, valeurs exactes.

Exercice N°630 :

Exercice, trigonométrie, équations, sinus, cosinus, première

Exercice N°630 :

1) Résoudre dans l’intervalle ]-π ; π] l’équation trigonométrique « sinus » suivante
sin(x) = √3/2
en détaillant soigneusement les étapes. Lis la suite »

Ecris le premier commentaire

Maths de première : exercice d’optimisation de l’aire d’un rectangle. Fonction, dérivation, tableau de variation, surface maximale.

Exercice N°793 :

Exercice, optimisation, aire, rectangle, tableau, variation, première, Route de Murat à Riom-ès-Montagle, Cantal, France

Exercice N°793 :

Le plan est muni d’un repère orthonormé.
On considère la droite d d’équation x = 12. On note C la courbe représentative de la fonction carré. Pour tout point M de coordonnées (x ; 0) avec x réel compris entre 0 et 12, on construit le rectangle ABCM comme le montre la figure ci-dessous.

Optimisation, aire, rectangle, tableau, variation, première, figure

1) Déterminer, en fonction de x, les coordonnées des points A, B et C. Lis la suite »

Ecris le premier commentaire

Maths : exercice d’optimisation de distance de première avec géométrie, fonction, dérivation, tableau de variation, maximum, triangle, carré.

Exercice N°792 :

Exercice, optimisation, distance, première, géométrie, dérivation

Exercice N°792 :

Soit f la fonction définie par :
f(x) = (x – x2)/(x + 1).

1) Donner le domaine de définition de la fonction f. Lis la suite »

Ecris le premier commentaire

Maths de première sur la trigonométrie : exercice d’équations avec sin et cos. Mesure principale, valeur exacte, polynôme du second degré.

Exercice N°629 :

Trigonométrie, valeurs, exercice, équations, sin, cos, première

Exercice N°629 :

1) Donner la valeur exacte de la valeur cos( -13π/3 ) en justifiant avec un schéma. Lis la suite »

Ecris le premier commentaire

Maths sur la trigonométrie : exercice sur les angles associés de première. Mesures principales, cosinus, sinus, valeurs exactes.

Exercice N°528 :

Exercice, angles associés, première, trigonométrie, cosinus, sinus

Exercice N°528 :

1) Donner la valeur exacte de cos( 31π/3 ) en détaillant les calculs et en justifiant à l’aide d’un schéma. Lis la suite »

Ecris le premier commentaire

Maths : exercice d’optimisation de surface de première. Dérivation, variation, extremum, carrés, fonction polynôme, affine, tableau de signe.

Exercice N°791 :

Exercice, optimisation, surface, première, variation, extremum

Exercice N°791 :

Soit un segment [AB] de longueur 10 et M un point de ce segment. Du même côté de ce segment, on construit deux carrés AMNP et MBCD.
On pose AM = x et on étudie la surface du domaine formé par ces deux carrés en fonction de x.

Optimisation, surface, première, variation, extremum, figure

1) À quel intervalle I appartient le réel x ? Lis la suite »

Ecris le premier commentaire

« Articles précédents     Articles suivants »
✕
FrenchMaths.com

GRATUIT
VOIR