Maths de première : exercice d’optimisation de surface d’un triangle avec dérivation, tableau de variation, polynôme, racine carrée.
Exercice N°796 :

Exercice N°796 :
Soit la fonction f définie sur R par :
f(x) = -x4 + 400x2.
1) Montrer que la fonction f est dérivable sur R et déterminer sa dérivée f ‘(x).
2) Établir le tableau de variation de la fonction f.
Soit ABC un triangle isocèle en A tel que AB = AC = 10.
On veut déterminer la longueur du segment [BC] afin que la surface de ce triangle soit maximale.
Voici le dessin du triangle ci-dessous :
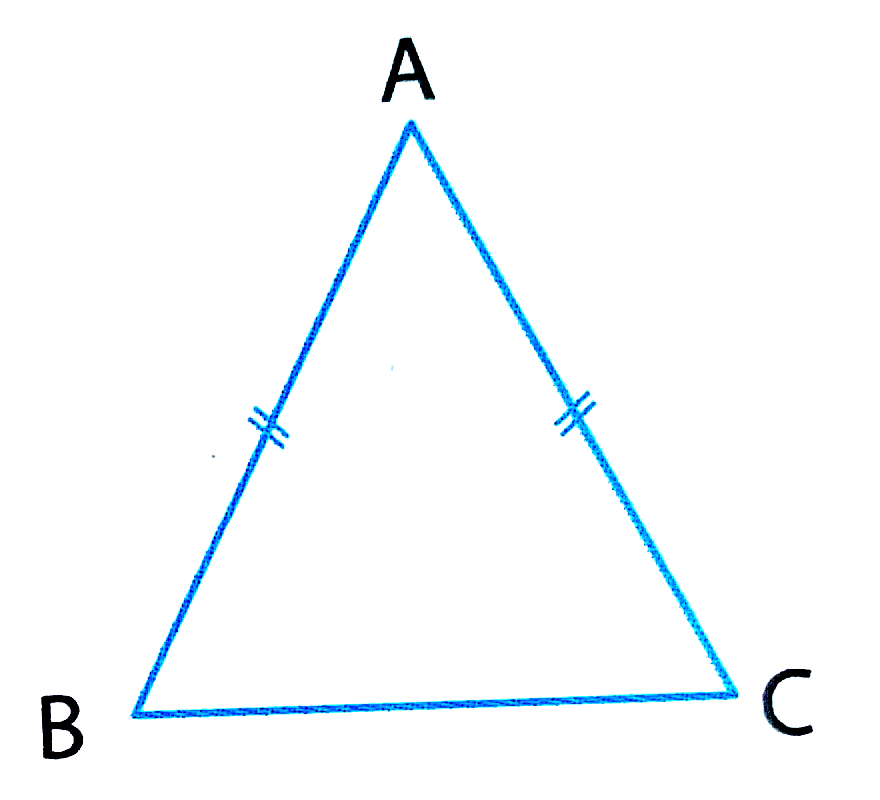
On appelle x la longueur BC.
3) Justifier que 0 ≤ x ≤ 20.
4) Exprimer l’aire S(x) du triangle ABC en fonction de x.
5) Justifier, que pour x allant de 0 à 20, on a :
f(x) ≤ 40000.
6) En remarquant que S(x) = (1/4)√f(x) pour 0 ≤ x ≤ 20, et à l’aide de la croissance de la fonction “racine”, déterminer la valeur maximale de la surface S(x) et la valeur de x pour laquelle elle est atteinte.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, optimisation, surface, triangle.
Exercice précédent : Optimisation – Aire, triangle, tableau de variation, maximum – Première

