Maths de seconde : exercice d’algorithme avec symétrique, milieu, géométrie du plan avec formules, coordonnées, variables.
Exercice N°586 :
Exercice N°586 :
On considère l’algorithme suivant :
Maths de première : exercice sur loi des sinus. Application du produit scalaire avec loi des sinus, théorème d’Al-Kashi, relation de Chasles.
Exercice N°672 :
Exercice N°672 :
Les bateaux d’Antonin (A) et de Brieuc (B) approchant de deux îles nommées C et D relèvent les mesures données sur le schéma ci-dessous.
On admet que le navire de Brieuc (B) est situé à 654,72 m de l’île D.
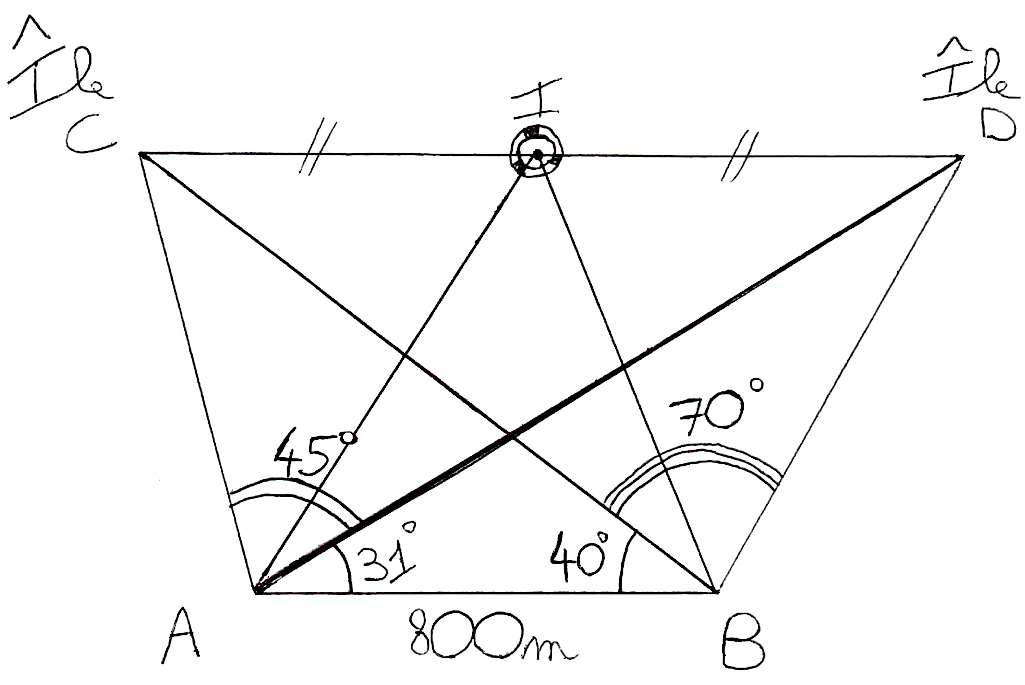
1) Déterminer la distance entre le navire de Brieuc et l’île C. Lis la suite »
Produits scalaires – Deux droites perpendiculaires – Première
1 décembre 2022
Exercice de maths de première. Produit scalaire, droites perpendiculaires. Vecteurs, géométrie dans le plan, repérage, démonstration.
Exercice N°073 :
Exercice N°073 :
ABCD est un carré.
M est un point du segment [AC] distinct de A et C.
P et Q sont les projetés orthogonaux de M respectivement sur (AD) et (CD).
Partie A :
1) Montrer que
→BQ.→CP = -BC × DP + CQ × CD. Lis la suite »
Maths de seconde : exercice d’algorithme avec du repérage de seconde. Formules de géométrie, rédaction, variables, triangle isocèle.
Exercice N°585 :
Exercice N°585 :
Le plan est muni d’un repère orthonormé (O ; I ; J).
A(xA ; yA), B(xB ; yB) et C(xC ; yC) sont trois points du plan.
1) Compléter l’algorithme suivant, en rapport avec le chapitre Repérage, en expliquant ce qu’il fait. Lis la suite »
Maths de première : exercice d’optimisation de surface d’un triangle avec dérivation, tableau de variation, polynôme, racine carrée.
Exercice N°796 :
Exercice N°796 :
Soit la fonction f définie sur R par :
f(x) = -x4 + 400x2.
1) Montrer que la fonction f est dérivable sur R et déterminer sa dérivée f ‘(x). Lis la suite »
Maths de première : exercice d’optimisation de l’aire d’un triangle avec dérivation, tableaux de signe et de variation, trouver le maximum.
Exercice N°795 :
Exercice N°795 :
Dans un repère orthonormé du plan, on considère la parabole P d’équation
y = -(2/9)x2 + 8.
La parabole est représentée graphiquement sur le schéma ci-dessous :
La parabole coupe l’axe des abscisses en les points A(-6 ; 0) et B(6 ; 0). Soit un point M sur l’arc de parabole compris entre les points A et B et H son projeté orthogonale sur le segment [AB].
On considère la fonction f définie sur l’intervalle [-6 ; 6] par l’expression :
f(x) = -(1/9)x3 – -(2/3)x2 + 4x + 24.
1) Montrer que l’aire du triangle AMH est égale à l’expression f(x). Lis la suite »
Maths de première : exercice d’optimisation du volume d’une boîte. Hauteur, dérivation, tableau de signe, tableau de variation, maximum.
Exercice N°794 :
Exercice N°794 :
On entoure une boîte avec un ruban de longueur totale 1.20 m dont 20 cm ont permis de réaliser le noeud. La boîte est un pavé droit à base carrée et le ruban passe par le milieu des arêtes des faces supérieures et inférieures, comme c’est indiqué sur le schéma ci-dessous.
On désigne par x la longueur du côté du carré (en mètre) et on désigne par h la hauteur de la boîte (en mètre).
1) Montrer que l’on a l’égalité :
4x + 4h = 1. Lis la suite »
Maths de première : exercice d’optimisation de l’aire d’un rectangle. Fonction, dérivation, tableau de variation, surface maximale.
Exercice N°793 :
Exercice N°793 :
Le plan est muni d’un repère orthonormé.
On considère la droite d d’équation x = 12. On note C la courbe représentative de la fonction carré. Pour tout point M de coordonnées (x ; 0) avec x réel compris entre 0 et 12, on construit le rectangle ABCM comme le montre la figure ci-dessous.
1) Déterminer, en fonction de x, les coordonnées des points A, B et C. Lis la suite »
Maths : exercice d’optimisation de distance de première avec géométrie, fonction, dérivation, tableau de variation, maximum, triangle, carré.
Exercice N°792 :
Exercice N°792 :
Soit f la fonction définie par :
f(x) = (x – x2)/(x + 1).
1) Donner le domaine de définition de la fonction f. Lis la suite »
Maths : exercice d’optimisation de surface de première. Dérivation, variation, extremum, carrés, fonction polynôme, affine, tableau de signe.
Exercice N°791 :
Exercice N°791 :
Soit un segment [AB] de longueur 10 et M un point de ce segment. Du même côté de ce segment, on construit deux carrés AMNP et MBCD.
On pose AM = x et on étudie la surface du domaine formé par ces deux carrés en fonction de x.
1) À quel intervalle I appartient le réel x ? Lis la suite »
