Maths de première : exercice sur loi des sinus. Application du produit scalaire avec loi des sinus, théorème d’Al-Kashi, relation de Chasles.
Exercice N°672 :

Exercice N°672 :
Les bateaux d’Antonin (A) et de Brieuc (B) approchant de deux îles nommées C et D relèvent les mesures données sur le schéma ci-dessous.
On admet que le navire de Brieuc (B) est situé à 654,72 m de l’île D.
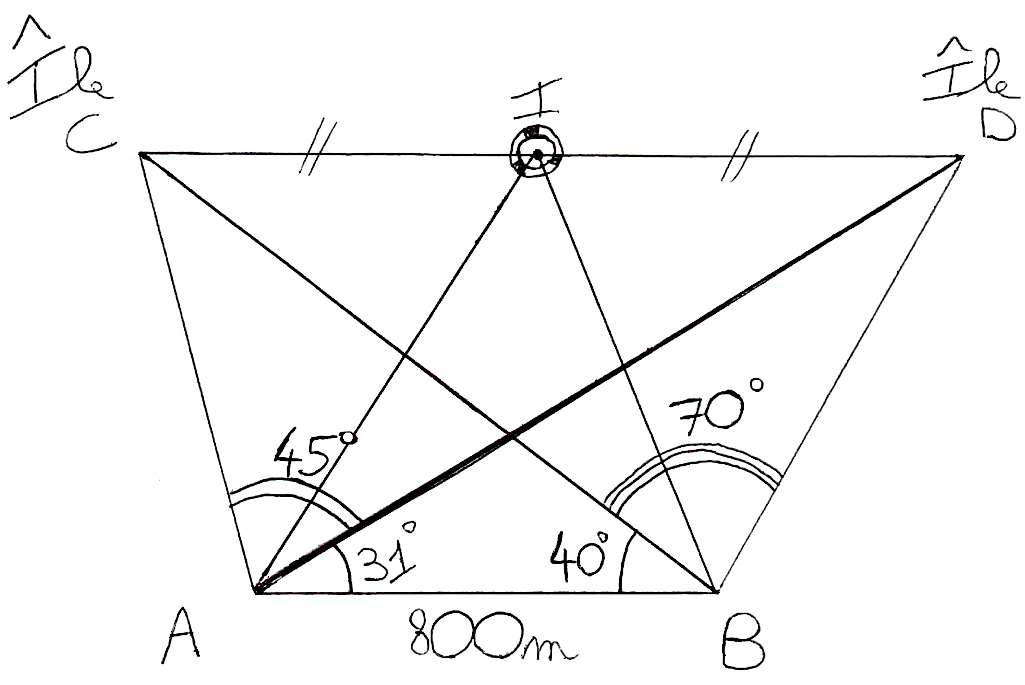
1) Déterminer la distance entre le navire de Brieuc et l’île C.
2) En déduire la distance entre les deux îles.
On considère que la course est terminée lorsqu’un bateau atteint la bouée située au milieu (I) des deux îles.
3) Déterminer la distance restante à parcourir pour Brieuc (B).
On admet que AI = 824,75.
4) Sachant que le bateau d’Antonin avance à une vitesse de 80 km/h et que celui de Brieuc avance à 50 km/h, qui gagnera la course ?
Partie indépendante sur les cosinus :
Soit ABC un triangle avec AB = c, AC = b et BC = a.
5) Sachant que B^AC = π/6, A^BC = π/6 et a = 1, calculer b.
6) Sachant que B^AC = 2π/3, b = 1 et c = 2, calculer a.
7) Sachant que B^AC = π/3, a = √3 et b = 1, calculer l’aire du triangle.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, loi des sinus.
Exercice précédent : Produits scalaires – Formules, orthogonaux, cosinus, normes – Première

