Maths de première : exercice d’optimisation de l’aire d’un rectangle. Fonction, dérivation, tableau de variation, surface maximale.
Exercice N°793 :

Exercice N°793 :
Le plan est muni d’un repère orthonormé.
On considère la droite d d’équation x = 12. On note C la courbe représentative de la fonction carré. Pour tout point M de coordonnées (x ; 0) avec x réel compris entre 0 et 12, on construit le rectangle ABCM comme le montre la figure ci-dessous.
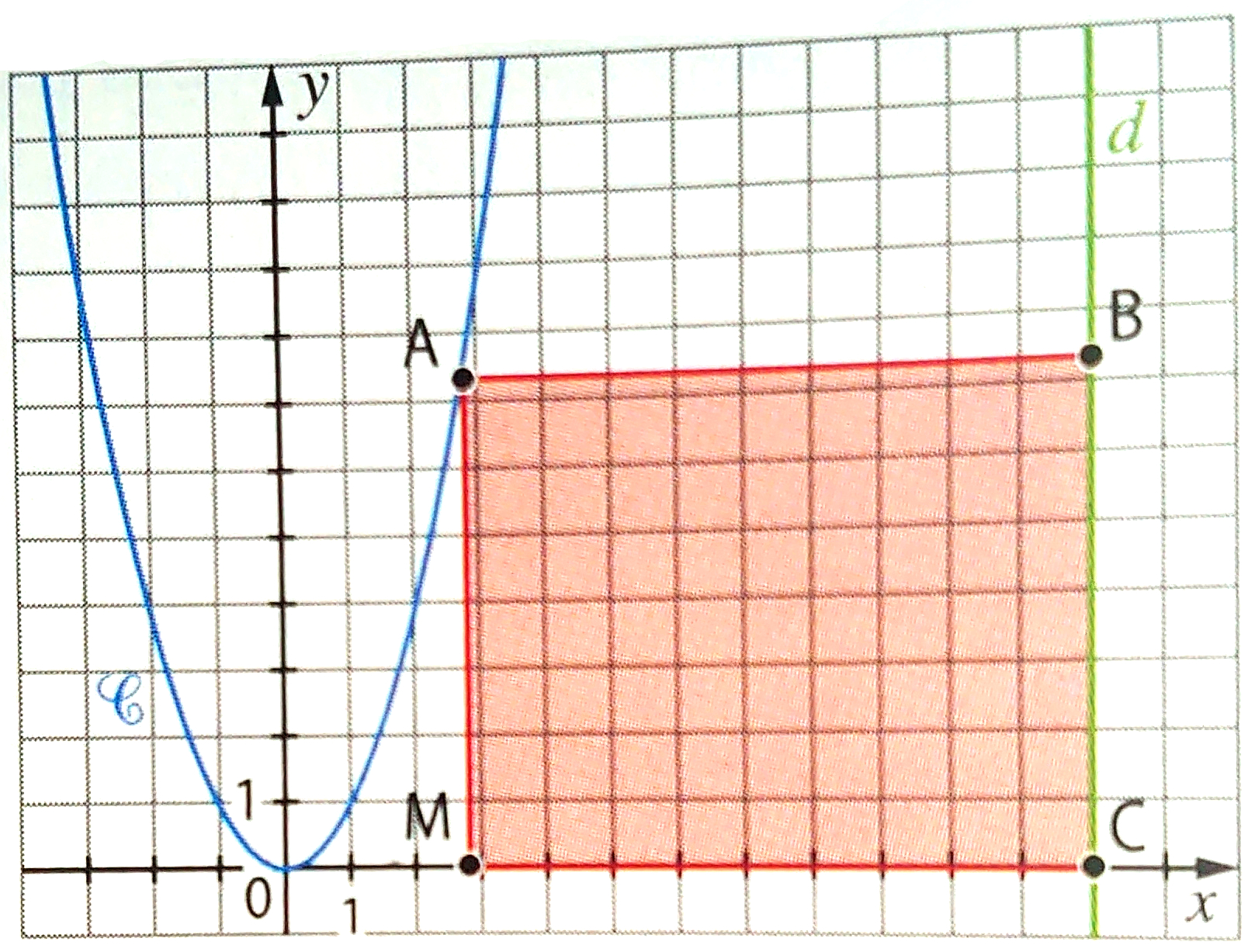
1) Déterminer, en fonction de x, les coordonnées des points A, B et C.
2) Montrer que l’aire du rectangle ABCM est égale à :
-x3 + 12x2.
On considère la fonction f définie sur [0 ; 12] par l’expression :
f(x) = -x3 + 12x2.
3) Déterminer la fonction dérivée f ‘(x) et étudier son signe en faisant un tableau de signe.
4) Étudier les variations de la fonction f sur l’intervalle [0 ; 12].
5) Déterminer la position du point M rendant l’aire du rectangle ABCM maximale.
6) Quelle est l’aire maximale du rectangle ABCM ?
7) Tracer dans un repère la courbe de la fonction “aire” f pour des valeurs de x allant de 0 à 12 sur l’axe des abscisses.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, optimisation, aire, rectangle.
Exercice précédent : Optimisation – Distance, géométrie, dérivation, triangle – Première

