Maths : exercice d’optimisation de distance de première avec géométrie, fonction, dérivation, tableau de variation, maximum, triangle, carré.
Exercice N°792 :

Exercice N°792 :
Soit f la fonction définie par :
f(x) = (x – x2)/(x + 1).
1) Donner le domaine de définition de la fonction f.
2) Montrer que la dérivée de la fonction f a pour expression :
f ‘(x) = (-x2 – 2x + 1)/(x + 1)2.
3) Déterminer le tableau de variation de la fonction f. Donner une valeur approchée des extremums locaux au centième près.
ABCD est un carré de côté 1.
E est un point de la demi-droite [DA) n’appartenant pas au segment [DA].
F est le point appartenant au segment [DC] et vérifiant AE = CF.
Le point d’intersection des droites (AB) et (EF) est noté I.
On note AE = CF = x et on étudie la surface du domaine formé par ces deux carrés en fonction de x.
Voici la figure ci-dessous :
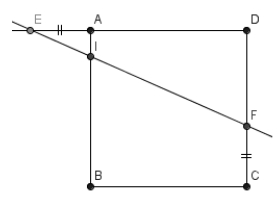
4) Démontrer que AI = (x – x2)/(x + 1).
5) En déduire la position du point E pour que la distance AI soit maximale.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, optimisation, distance, première.
Exercice précédent : Optimisation – Dérivation, surface, variation, extremum – Première

