Maths : exercice d’optimisation de surface de première. Dérivation, variation, extremum, carrés, fonction polynôme, affine, tableau de signe.
Exercice N°791 :

Exercice N°791 :
Soit un segment [AB] de longueur 10 et M un point de ce segment. Du même côté de ce segment, on construit deux carrés AMNP et MBCD.
On pose AM = x et on étudie la surface du domaine formé par ces deux carrés en fonction de x.
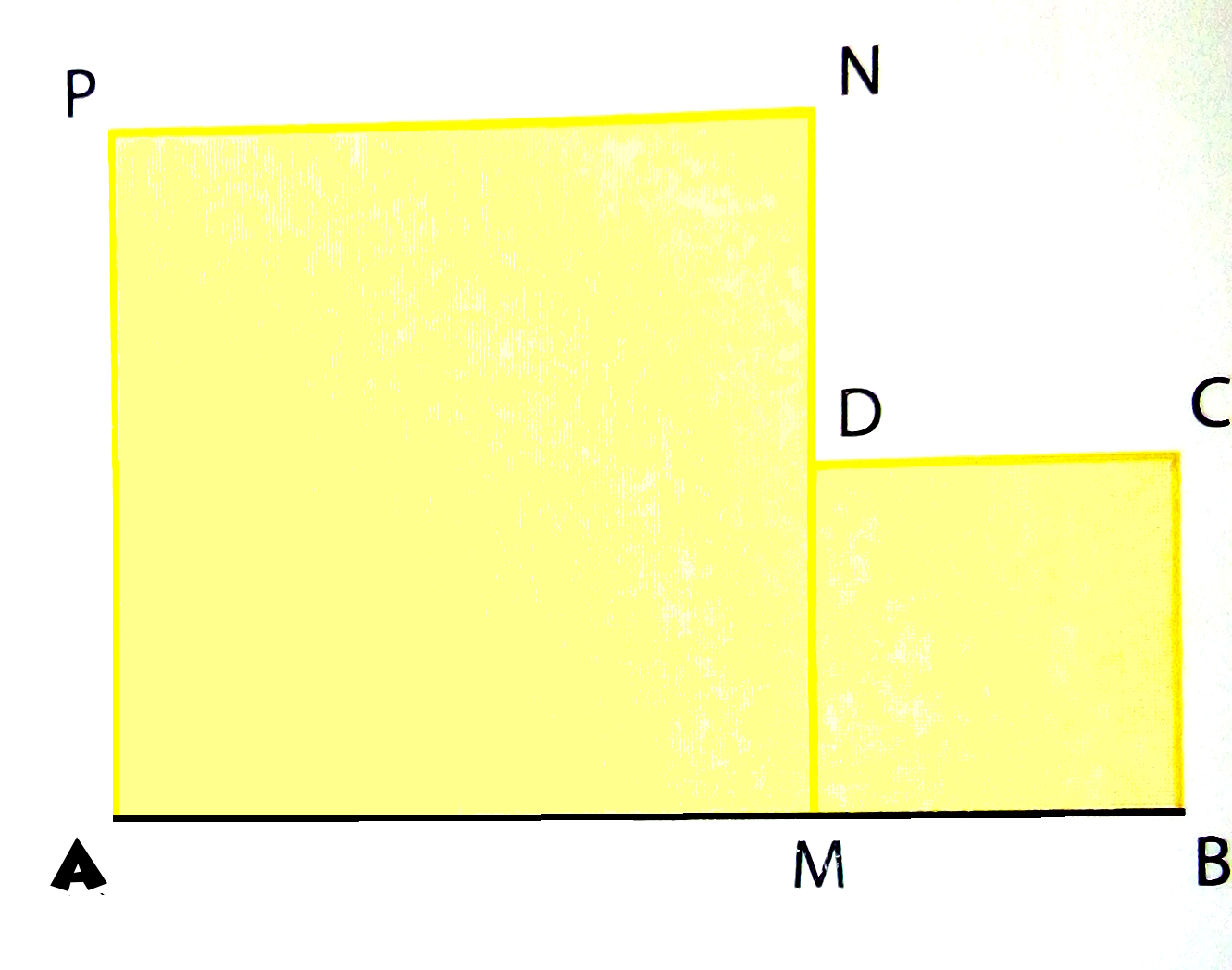
1) À quel intervalle I appartient le réel x ?
Soit f(x) la surface du domaine.
2) Montrer que, pour tout réel x de I, on a :
f(x) = 2x2 – 20x + 100.
3) Justifier que la fonction f est dérivable sur I et
calculer la fonction dérivée f ‘(x) pour tout x de I.
4) En déduire les variations de f sur I.
5) La surface des deux carrées admet-elle comme extremum, un minimum ou un maximum ?
6) En quel valeur de x, cet extremum est-il atteint ?
7) Quel est la valeur de cet extremum ?
8) Tracer la courbe de la surface f(x) dans un repère orthonormé pour les valeurs comprises dans l’intervalle I.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, optimisation, surface, première.
Exercice précédent : Optimisation – Aire, dérivation, variation, surface – Première

