Maths : exercice d’optimisation de l’aire en première. Dérivation, tableau de variation, surface de carrés, maximum, minimum, extremum.
Exercice N°790 :

Exercice N°790 :
Sur la figure ci-dessous, ABCD et BEFG sont des carrés tels que B appartient au segment [AE] et C appartient au segment [GB]. De plus, [AE] = 4 cm. Le but est de déterminer la valeur de x telle que la somme des aires de ces deux carrés est maximale ou minimale.
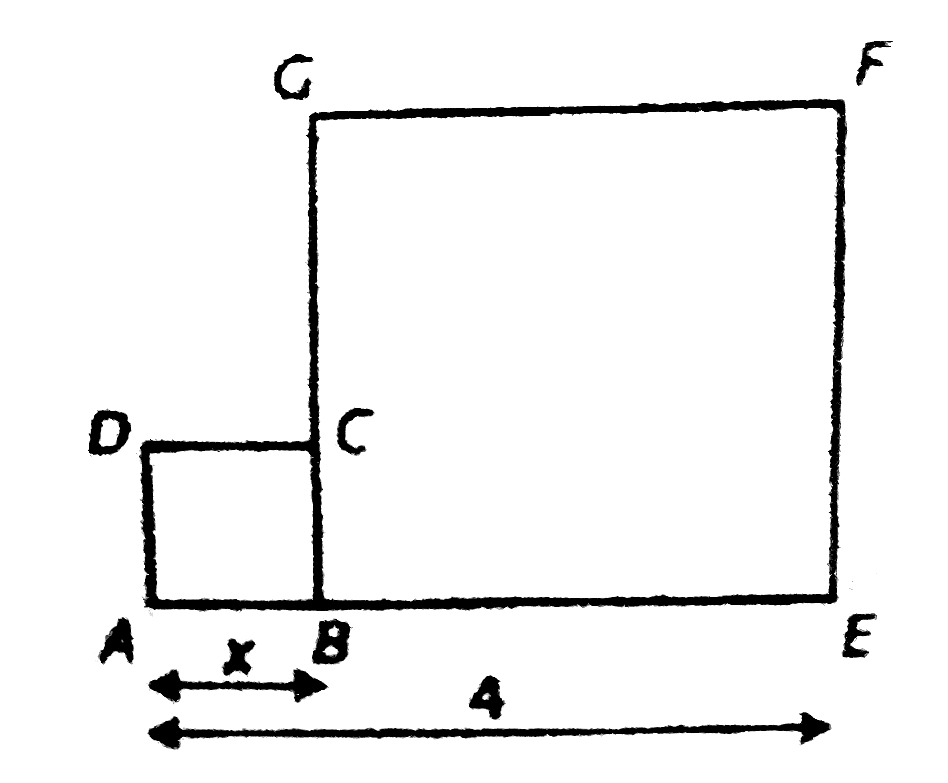
1) À quel intervalle I appartient le réel x ?
2) Exprimer l’aire du carré ABCD en fonction du réel x.
3) Exprimer la longueur BE en fonction du réel x.
4) En déduire l’aire du carré BEFG en fonction du réel x.
5) Montrer que la somme des aires des deux carrés en fonction de x est donnée par une fonction f sur l’intervalle I dont l’expression est :
f(x) = 2x2 – 8x + 16.
6) Calculer la fonction dérivée f ‘(x) de la fonction f(x).
7) Donner le tableau de variation complet de la fonction f sur l’intervalle I.
8) Cette aire admet-elle des extremums locaux ? Des extremums globaux ? Préciser lesquels.
9) Tracer la courbe représentative de la fonction f.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, optimisation, aire, première.
Exercice précédent : Optimisation – Volume de boîte, dérivation, variation – Première

