Maths : exercice d’optimisation de volume en première. Pavé droit, fonction, dérivation, tableau de variation, maximum, tracer la courbe.
Exercice N°789 :

Exercice N°789 :
Une pâtissière présente ses tartelettes à la fraise dans une boîte dont la partie inférieure, ouverte sur le dessus, est confectionnée de la manière suivante :
Tout d’abord, elle dispose d’un carton de forme carrée de 20 centimètres de côté.
Ensuite, elle découpe dans chaque coin un carré de côté x centimètre(s), et replie suivant les pointillés pour obtenir sa boîte en forme de parallélépipède rectangle.
Le schéma de la boîte est représenté ci-dessous :
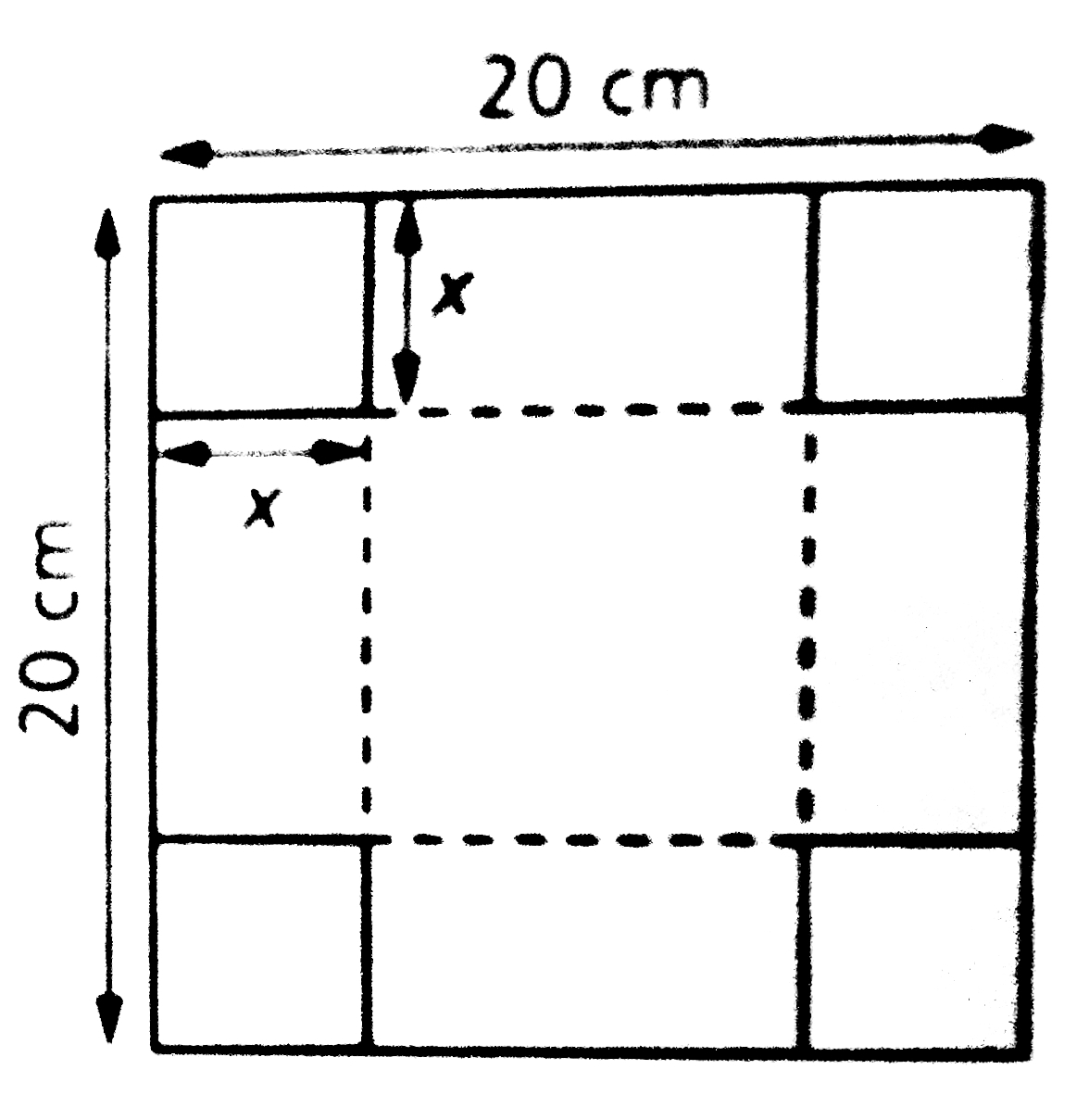
1) Déterminer dans quelle intervalle I le réel x peut varier.
2) Démontrer que le volume de la boîte est donné par V = f(x) où f est la fonction définie sur l’intervalle I par :
f(x) = x(2x – 20)2.
3) Calculer la fonction dérivée f ‘(x) de la fonction f(x).
4) Étudier les variations de la fonction f sur l’intervalle I.
5) Démontrer qu’il existe une valeur de x, notée a, en laquelle le volume de la boîte est maximum.
6) Tracer la courbe représentative de la fonction f.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, optimisation, volume, première.
Exercice précédent : Dérivation – Trouver les coefficients d’un polynôme – Première

