Maths de première : exercice de dérivation pour trouver les coefficients d’une fonction polynôme avec représentation graphique à tracer.
Exercice N°788 :

Exercice N°788 :
Le responsable d’une station de ski souhaite construire un nouveau tire-fesses entre deux zones planes de sa station. Le projet est résumé sur le schéma ci-dessous où les deux points à relier sont O et A.
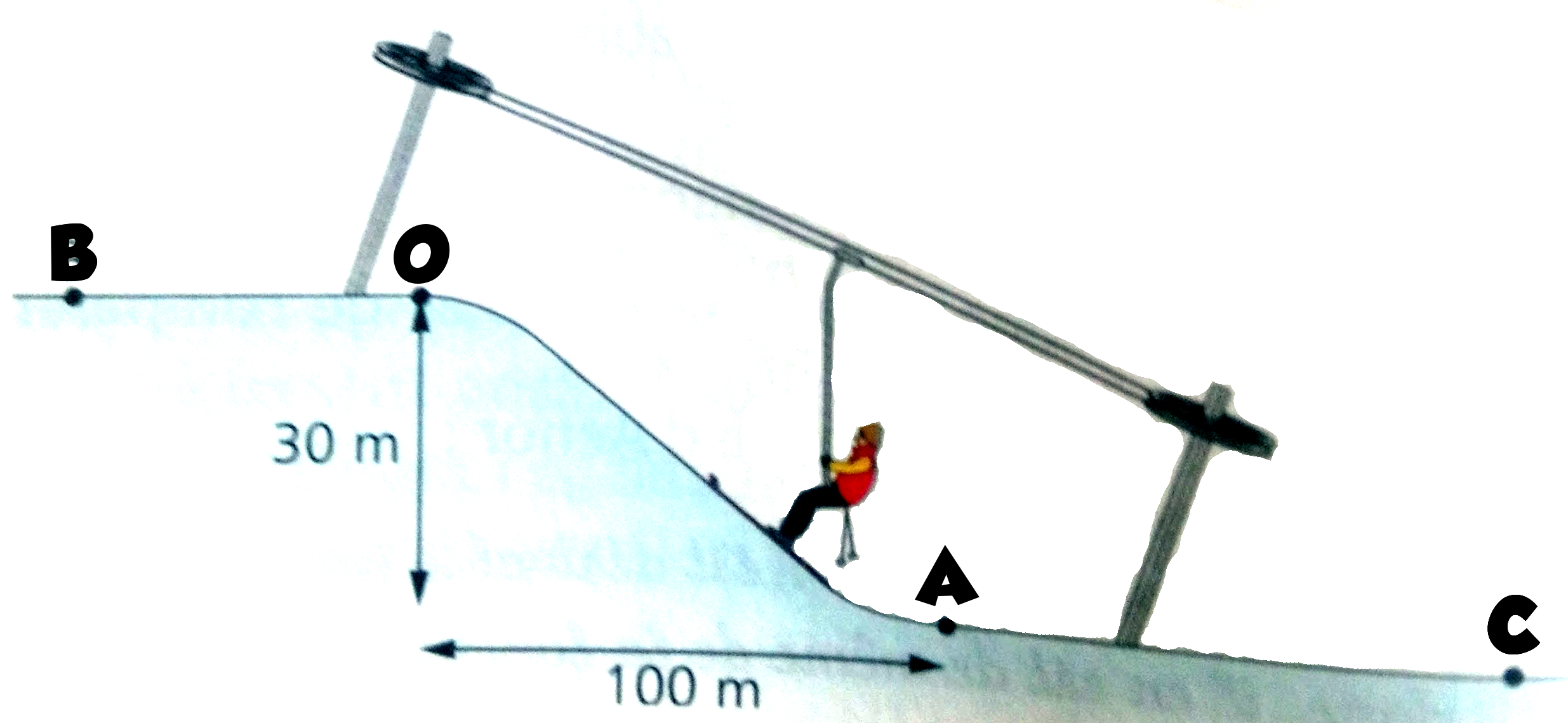
Pour résoudre ce problème, on se place dans un repère orthonormal (O ; I ; J) dans lequel A possède les coordonnées (0 ; -30), et on désigne par f la fonction définie sur [0 ; 100] donc la courbe représentative est donnée sur le schéma du dessus.
Le responsable souhaiterais que le départ et l’arrivée du tire-fesses se fassent “sans cassure”, autrement dit que la fonction f soit dérivable sur l’intervalle [0 ; 100].
1) Déterminer les valeurs f(0) et f(100) en justifiant..
2) Déterminer les valeurs f ‘(0) et f ‘(100) en justifiant.
On suppose qu’il existe trois réels a, b et c tel que, pour tout réel x appartenant à l’intervalle [0 ; 100] :
f(x) = ax2 + bx + c.
3) Déduire des valeurs f ‘(0) et f ‘(100) que les réels a et b sont nuls.
4) Démontrer que f est la fonction nulle, puis conclure que la fonction f cherchée ne peut pas être une fonction de degré 2.
On suppose qu’il existe quatre réels m, n, p et q tel que, pour tout réel x appartenant à l’intervalle [0 ; 100] :
f(x) = mx3 + nx2 + px + q
où m, n, p et q sont des nombres réels.
5) Déterminer que les valeurs de f(0) et de
f ‘(0) permettent d’obtenir p = q = 0.
6) Trouver alors les valeurs m et n à l’aide des valeurs de f(100) et de
f ‘(100).
7) En déduire l’expression de la fonction f.
8) Tracer la courbe représentative de la fonction f lorsque x varie de 0 à 100.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivation, trouver coefficients.
Exercice précédent : Dérivation – Coefficients, polynôme, équation, tangente – Première

