Maths de première : exercice de dérivation avec coefficients de polynôme à trouver. Équations, tangente, variation, factorisation, tableaux.
Exercice N°787 :

Exercice N°787 :
Voici une portion de la courbe représentative C d’une fonction f définie sur R par :
f(x) = mx3 + nx2 + px + q
où m, n, p et q sont des nombres réels.
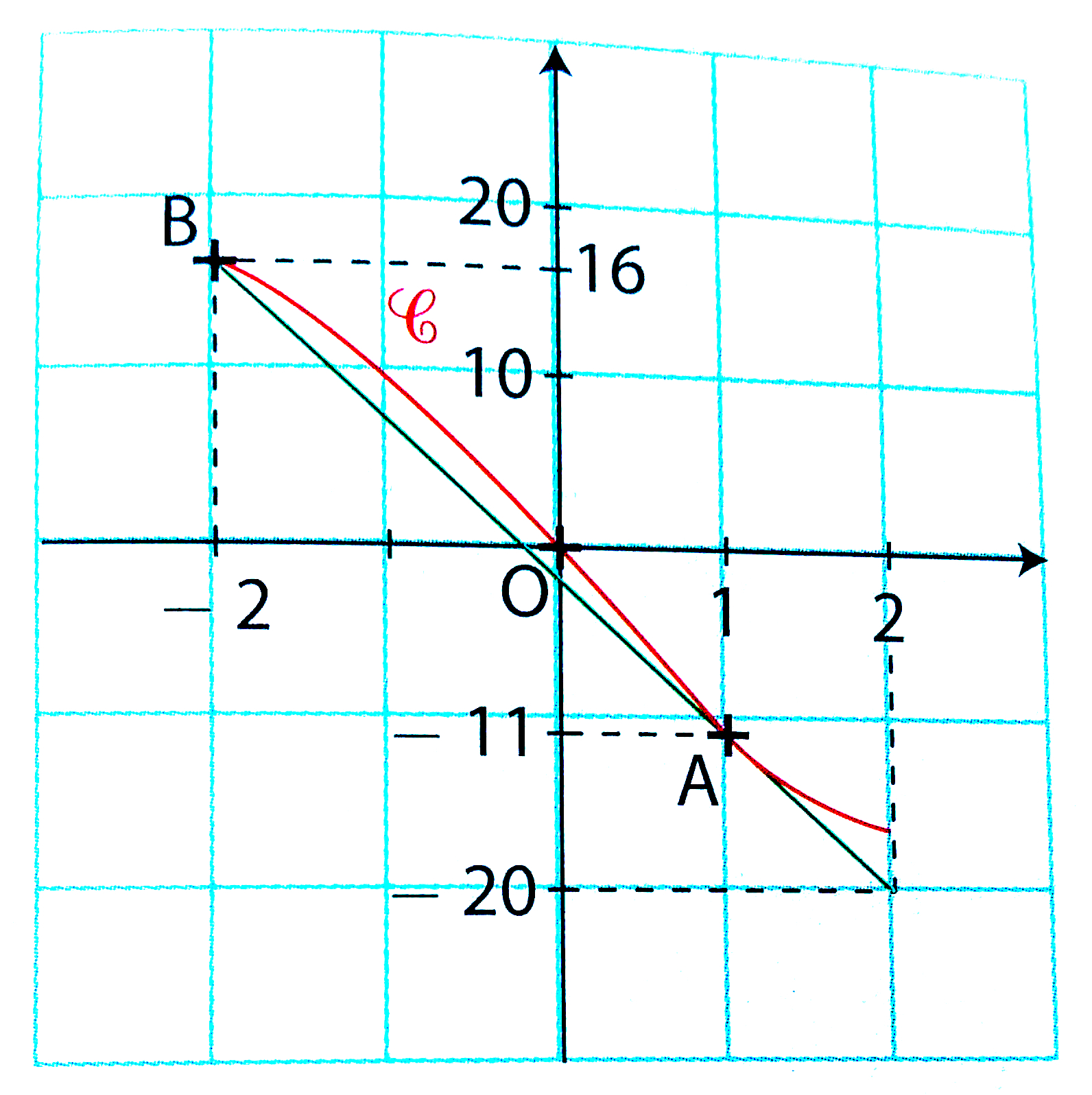
La droite [AB] est tangente à C au point A(1 ; -11) et la tangente à C en O a pour équation :
y = -12.
1) Déterminer la valeur de f(0).
2) Déterminer la valeur de f ‘(0).
3) Déterminer la valeur de f(1).
4) Déterminer la valeur de f ‘(1).
5) En utilisant les résultats des questions 1) et 2), déterminer p et q.
6) En utilisant les résultats des questions 3) et 4), déterminer m et n
7) Étudier les variations de la fonction f.
Partie indépendante :
Soit la fonction g définie sur R par :
g(x) = 12x3 + (5/2)x2 − x + 80.
8) Calculer la fonction dérivée de g.
9) Démontrer que g ‘(x) = 36(x + 1/4)(x – 1/9).
10) Déterminer le signe de g ‘(x) en fonction de x.
11) Dresser le tableau de variation de g.
12) Représenter graphiquement la fonction g.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivation, coefficients, polynôme.
Exercice précédent : Dérivation – Géométrie, aire, variation, tableaux, signe – Première

