Maths de première : exercice de dérivation avec géométrie et variation. Tableau de signe, factorisation, surfaces, polynômes, racines.
Exercice N°786 :

Exercice N°786 :
1-2-3) Sur la figure ci-dessous, ABCD est un carré, de côté 4, M est un point mobile du segment [AB]. AMEF est un carré, H est un point du segment [CD] tel que MBH soit isocèle en H. On pose x = AM.
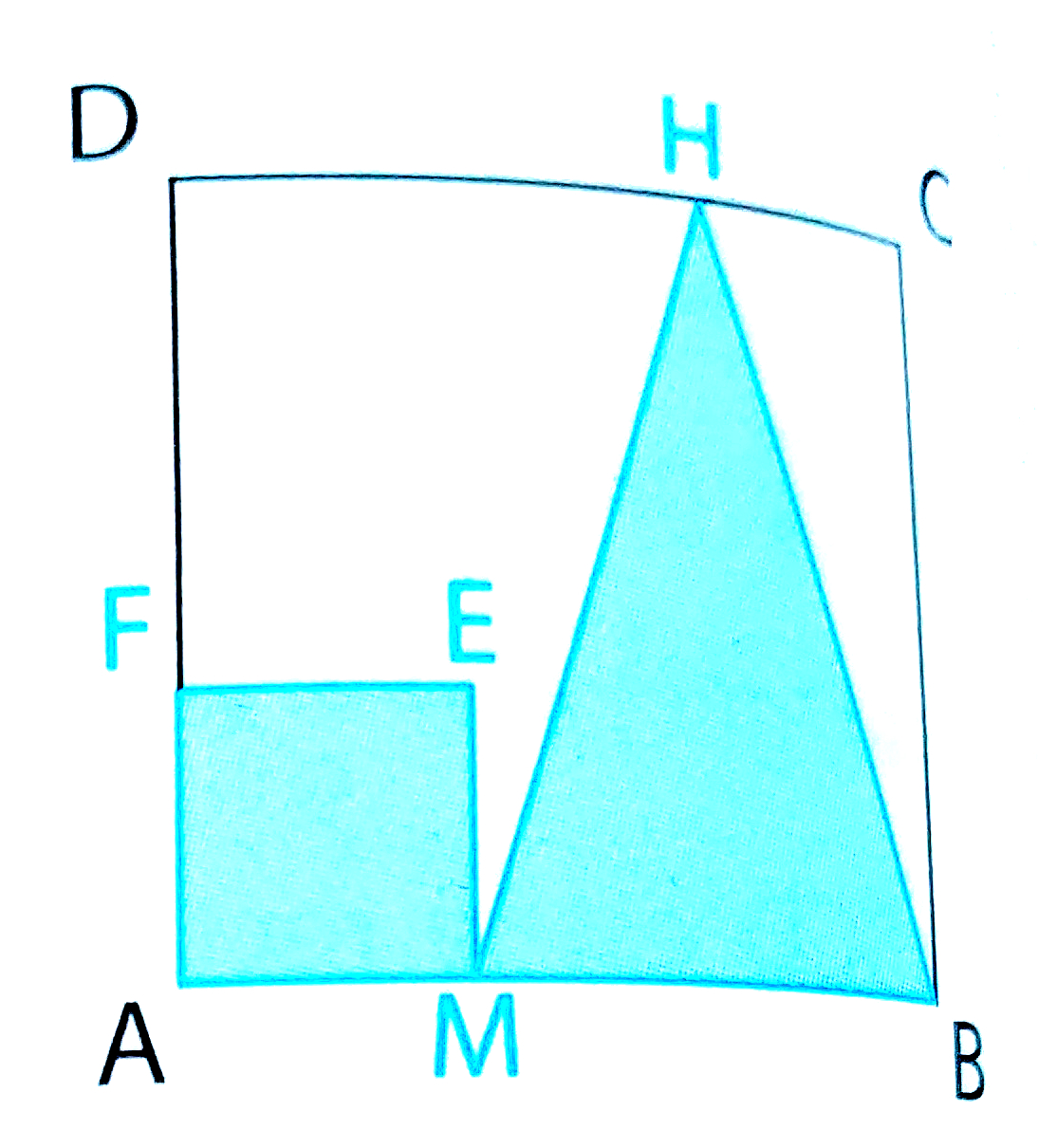
1) Démontrer que l’aire du domaine coloré est donnée par
f(x) = x2 – 2x + 8.
2) Étudier les variations de la fonction f sur l’intervalle [0 ; 4].
Élia affirme : “L’aire du domaine coloré occupe toujours au moins 40 % de l’aire du carré ABCD.
3) Que peut-on penser de l’affirmation d’Élia ? Justifier la réponse.
4-5-6-7-8) Soit la fonction g définie sur R par :
g(x) = 2x3 + (7/2)x2 − 3x + 2.
4) Calculer la fonction dérivée de g.
5) Démontrer que g ‘(x) = 6(x – 1/3)(x + 3/2).
6) Déterminer le signe de g ‘(x) en fonction de x.
7) Dresser le tableau de variation de g.
8) Représenter graphiquement la fonction g.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivation, géométrie, variation.
Exercice précédent : Géométrie 2D – Équations, cercles, figure, tangentes – Première

