Maths de première : exercice d’optimisation de l’aire d’un triangle avec dérivation, tableaux de signe et de variation, trouver le maximum.
Exercice N°795 :

Exercice N°795 :
Dans un repère orthonormé du plan, on considère la parabole P d’équation
y = -(2/9)x2 + 8.
La parabole est représentée graphiquement sur le schéma ci-dessous :
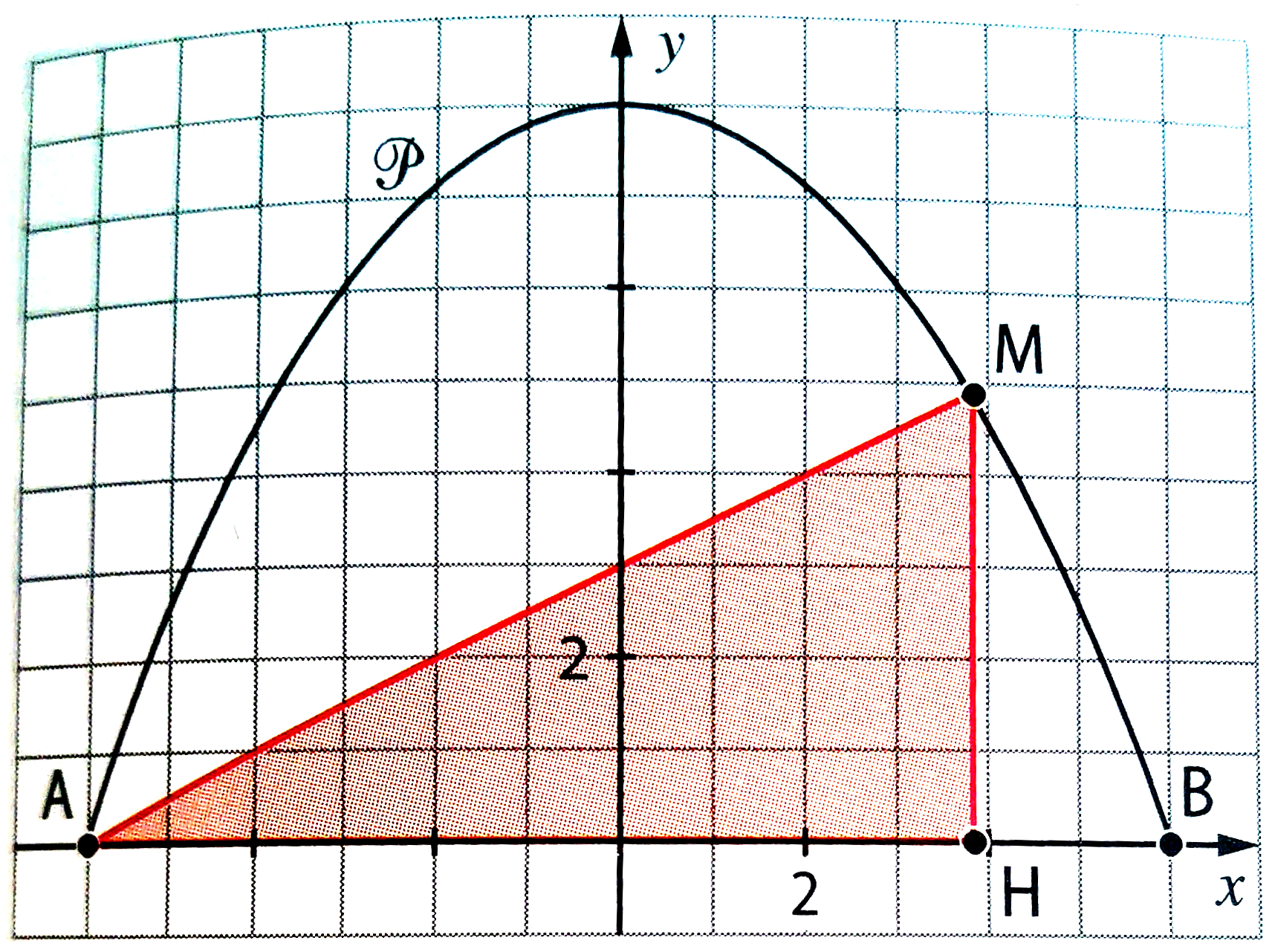
La parabole coupe l’axe des abscisses en les points A(-6 ; 0) et B(6 ; 0). Soit un point M sur l’arc de parabole compris entre les points A et B et H son projeté orthogonale sur le segment [AB].
On considère la fonction f définie sur l’intervalle [-6 ; 6] par l’expression :
f(x) = -(1/9)x3 – -(2/3)x2 + 4x + 24.
1) Montrer que l’aire du triangle AMH est égale à l’expression f(x).
2) Déterminer la fonction dérivée f ‘(x) sur l’intervalle [-6 ; 6].
3) Étudier le signe de f ‘(x) en faisant un tableau de signe.
4) Étudier les variations de la fonction f sur l’intervalle [-6 ; 6].
5) Déterminer la position de M pour laquelle l’aire du triangle AMH est maximale.
6) Représenter dans un repère orthonormé la courbe de l’aire du triangle sur l’intervalle [-6 ; 6].
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, optimisation, aire, triangle.
Exercice précédent : Optimisation – Volume, boîte, hauteur, dérivation, maximum – Première

