Exercice de maths de première. Produit scalaire, droites perpendiculaires. Vecteurs, géométrie dans le plan, repérage, démonstration.
Exercice N°073 :

Exercice N°073 :
ABCD est un carré.
M est un point du segment [AC] distinct de A et C.
P et Q sont les projetés orthogonaux de M respectivement sur (AD) et (CD).
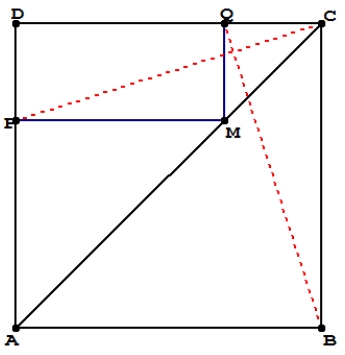
Partie A :
1) Montrer que
→BQ.→CP = -BC × DP + CQ × CD.
2) Démontrer que DP = CQ.
3) Démontrer que les droites (BQ) et (CP) sont perpendiculaires.
Partie B indépendante de A :
Dans le repère orthonormé (A ; →AB ; →AD), on note x l’abscisse du point M.
4) Justifier que le point M a pour coordonnées (x ; x) avec 0 < x < 1.
5) Déterminer les coordonnées des points B, C, P et Q dans ce repère.
6) Calculer →BQ.→CP.
7) Démontrer que les droites (BQ) et (CP) sont perpendiculaires.
Questions indépendantes :
8-9-10-11) Pour chaque affirmation répondre par VRAI ou FAUX en justifiant votre réponse.
8) →u(3/4 ; -1) et →v(7/3 ; 7/4) sont orthogonaux.
9) →v(-2 ; 3) est le seul vecteur orthogonal à →u(3 ; 2).
10) Si ||→u + →v||2 = ||→u||2 + ||→v||2, alors →u et →v sont orthogonaux.
11) Si ||→u + →v|| = ||→u|| + ||→v||, alors →u et →v ne sont pas orthogonaux.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : produit scalaire, droites perpendiculaires.
Exercice précédent : Vecteurs – Figures, démonstrations, alignement de points – Première

