Maths de terminale : exercice d’exponentielle avec continuité et équation. Tableau de variation, solution unique, encadrement.
Exercice N°750 :
Exercice N°750 :
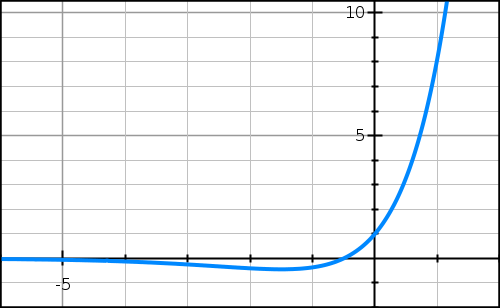
On considère la fonction f définie sur R par
f(x) = (-4x2 + 5)e-x + 3.
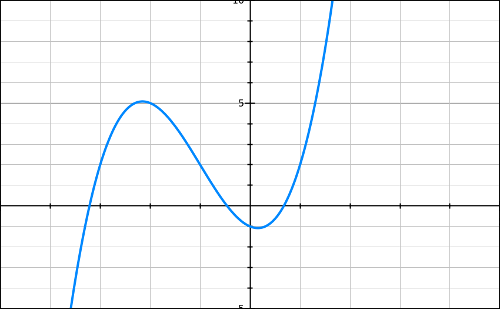
On note (C) la courbe représentative de la fonction f dans un repère orthogonal.
On note f ‘ la dérivée de f sur R.
1) Démontrer que pour tout réel x ∈ R,
f ‘ (x) = (4x2 – 8x – 5)e-x. Lis la suite »
Maths de terminale : exercice d’exponentielle avec variation et continuité, équation avec solution unique, coût de production, primitive.
Exercice N°749 :
Exercice N°749 :
Soit f la fonction définie sur [0 ; 5] par
f(x) = (ax + b)e−x
où a et b sont deux réels.
On note f ‘ la fonction dérivée de f.
1) Montrer que pour tout nombre réel x,
f ‘ (x) = (a − b − ax)e−x. Lis la suite »
Maths : exercice de convexité et exponentielle de terminale. Fonctions dérivées, signe, variation, convexe, concave, point d’inflexion.
Exercice N°747 :
On considère la fonction f définie sur R par l’expression :
f(x) = (2x + 1)ex.
1) Étudier le signe de la fonction f. Lis la suite »
Exercice de maths sur la convexité. Fonctions, taux, courbe, variations, calculer point d’inflexion, terminale, tangente, position relative.
Exercice N°305 :
Exercice N°305 :
Le tableau ci-dessous représente l’évolution du taux d’endettement des ménages, en pourcentage du revenu disponible brut, en France de 2001 à 2010.
Une estimation de l’évolution du taux d’endettement des ménages est modélisée par la fonction f définie sur l’intervalle [0 ; 11] par :
f(x) = −0,04x3 + 0,68x2 − 0,06x + 51,4
où x est le nombre d’années écoulées depuis 2000.
Ainsi, le taux d’endettement des ménages en % à la fin du premier semestre 2003 est estimé par f(2,5).
1) Calculer la valeur estimée du taux d’endettement des ménages en 2009. Lis la suite »
Maths : exercice de continuité et convexité de terminale. Dérivée, variation, point d’inflexion, équation, tangente, valeurs intermédiaires.
Exercice N°308 :
Exercice N°308 :
On considère la fonction f définie sur [0 ; 4] par
f(x) = 2x3 − 12x2 + 55
et on note Cf sa représentation graphique.
1) Calculer f ‘ (x) et f ‘ ‘ (x). Lis la suite »
Exercice de maths de terminale sur la convexité, dérivée seconde, inflexion, fonctions, courbe représentative, concave, convexe, variation.
Exercice N°306 :
Exercice N°306 :
Soit f une fonction deux fois dérivable sur [−2,5 ; 4].
On note f ‘ sa dérivée et f ‘ ‘ sa dérivée seconde.
La courbe représentative de la fonction dérivée notée Cf ‘ est donnée ci dessous.
La droite T est tangente à la courbe Cf ‘ au point d’abscisse 0.
Par lecture graphique :
1) Résoudre f ‘ (x) = 0.
En déduire le tableau de variations de f. Lis la suite »
Exercice de maths avec inéquation, quotient, second degré, fonction, courbe représentative, dénominateur, tableau de signe.
Exercice N°394 :
On donne les fonctions suivantes :
f1(x) = x²/2 – 2x + 3 pour x ∈ R,
f2(x) = (3x – 6)/(2x + 4) pour x ≠ 2,
f3(x) = –x²/2 + x + 3 pour x ∈ R,
f4(x) = (-2x + 2)/(3 – x) pour x ≠ 3,
f5(x) = x² + x – 4 pour x ∈ R.
1) Compléter les phrases suivantes par C1, C2, C3, C4 et C5 :
La fonction f1 a pour courbe représentative … . Lis la suite »
Maths de terminale : exercice de continuité en un point avec limite. Fonctions polynômes et rationnelles/fractions. Intervalles, expressions.
Exercice N°705 :
Exercice N°705 :
Soit f la fonction définie sur l’intervalle [−2 ; 3] par :
{ f(x) = −x2 + p, si x ∈ [−2; 1[
{ f(x) = 1/x , si x ∈ [1 ; 3].
1) Déterminer le nombre réel p afin que la fonction f soit continue sur l’intervalle [−2 ; 3]. Lis la suite »
Maths de terminale : exercice sur la convexité avec tangente et inflexion. Position relative, courbe, point, signe, dérivée seconde.
Exercice N°310 :
Exercice N°310 :
Soit la fonction définie sur [1 ; 5] par
f(x) = x3 – 6x² + 11x – 8.
On note Cf la courbe représentative de f.
1) Déterminer l’équation réduite de la tangente T2 à la courbe Cf au point d’abscisse 2. Lis la suite »
Maths de terminale : exercice de convexité avec point d’inflexion. Fonction polynôme, sa courbe, variations , équation de tangente.
Exercice N°309 :
On considère la fonction f définie sur [-3 ; 1.5] par l’expression
f(x) = x3 + 3x2 – x – 1.
Cette fonction est représentée ci-dessus.
1) Étudier les variations de la fonction f. Lis la suite »
