Maths : exercice de convexité et exponentielle de terminale. Fonctions dérivées, signe, variation, convexe, concave, point d’inflexion.
Exercice N°747 :
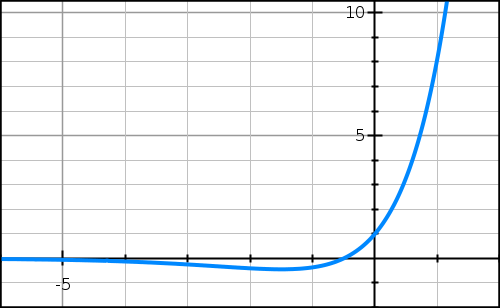
On considère la fonction f définie sur R par l’expression :
f(x) = (2x + 1)ex.
1) Étudier le signe de la fonction f.
2) Étudier les variations de la fonction f.
3) Étudier la convexité de la fonction f.
4) Donner les coordonnées des points d’inflexion éventuels de la courbe et l’équation de la tangente à la courbe de f en ces points.
g(x) = xex.
5) g est-elle convexe sur R ? g est-elle concave sur R ? La courbe Cg admet-elle un point d’inflexion ?
h(x) = ex/(x – 1).
6) Calculer h ‘ (x).
k(x) = 0,9x.
7) k est-elle une fonction croissante sur R ? k est-elle une fonction concave sur R ? k est-elle une fonction positive sur R ?
Bon courage,
Sylvain Jeuland
Pour avoir la suite du corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre Continuité et Convexité de Terminale (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, exponentielle, convexite, terminale.
Exercice précédent : Racine carrée – Fonction, domaine, signe, variation, graphique – Seconde

