Maths : exercice sur dérivée et exponentielle de terminale. Équations, inéquations, dérivées, limites, tableau de variations, asymptotes.
Exercice N°275 :
Exercice N°275 :
1-6) Résoudre les équations suivantes :
1) ex = -4, Lis la suite »
Exponentielle – Equation, dérivée, limite, variation – Terminale
12 octobre 2022
Suites – Conjecture, expression, limite, algorithme – Terminale
18 septembre 2022
Exercice de maths avec algorithme, terminale, conjecturer, suite. Repère, graphique, auxiliaire géométrique, premier terme, raison, limite.
Exercice N°212 :
Exercice N°212 :
On donne ci-dessous la représentation graphique des 16 premiers termes d’une suite (un) dans le plan muni d’un repère orthogonal.
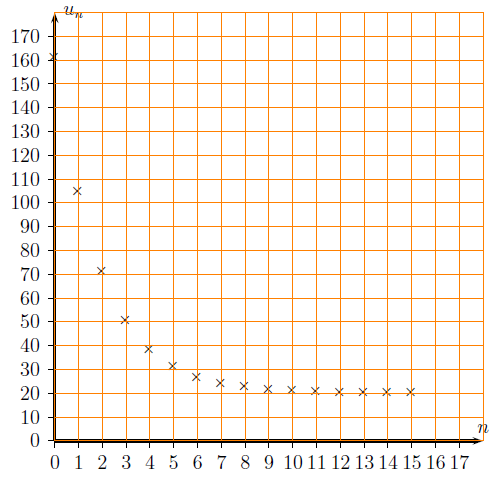
1) Conjecturer la limite de la suite (un). Lis la suite »
Maths : exercice de vecteurs et triangles de première. Formules, lecture graphique, milieux, repère, colinéarité, points alignés.
Exercice N°686 :
Triangle de gauche sur le dessin :
Sur le triangle ABC ci-dessous, les subdivisions sur les côtés sont régulières. Les points P, Q et R appartiennent respectivements aux droites (AB), (BC) et (AC).
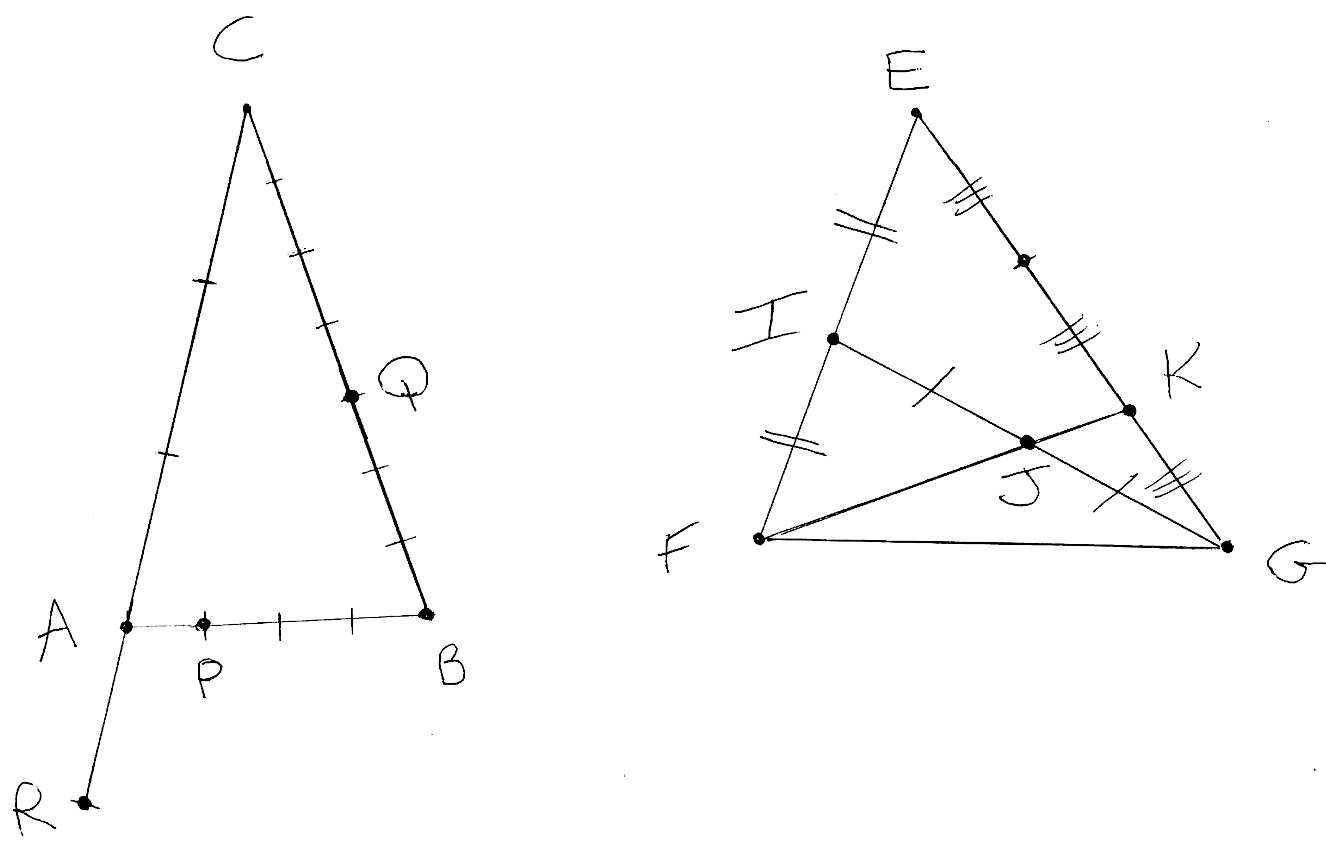
1) Déterminer par lecture graphique les réels x, y et z tels que :
→AP = x→AB,
→BQ = y→BC,
→AR = z→AC. Lis la suite »
Maths de terminale : exercice de limites de suites de première. Polynôme, fraction, sinus et puissances, infini, second et troisième degré.
Exercice N°661 :
Exercice N°661 :
1-6) Calculer les limites suivante en +∞ :
1) rn = -n3 + 7n2 – n + 2. Lis la suite »
Exponentielle – Équation, continuité, suite, récurrence – Terminale
13 novembre 2021
Exercice de maths sur la fonction exponentielle, suite, récurrence, terminale, continuité, équations, convergence, raisonnement, variations.
Exercice N°284 :
Exercice N°284 :
Le but de l’exercice est de démontrer que l’équation (E) ∶
xex = 1
admet une unique solution dans l’ensemble R des nombres réels, et de construire une suite qui converge vers cette unique solution.
Existence et unicité de la solution :
On note f la fonction définie sur R par
f(x) = x − e−x.
1) Démontrer que x est solution de l’équation (E)
si et seulement si f(x) = 0. Lis la suite »
Maths de terminale: Exercice de suite avec variation de fonction, récurrence, inégalités, termes, bornes, convergence, limite.
Exercice N°190 :
Exercice N°190 :
On modélise le nombre un de foyers français possédant un téléviseur à écran plat (en millions) en fonction de l’année (2005 + n) par la suite u définie par,
u0 = 1
et pour tout entier naturel n :
un+1 = (1/10)un(20 − un).
Soit la fonction f définie sur [0 ; 20] par :
f(x) = (1/10)x(20 − x).
1) Étudier les variations de f sur [0 ; 20]. Lis la suite »
Fonctions – Bases, limites, variations, équations – Terminale
30 septembre 2021
Maths de terminale : exercice, fonction, continuité, limite, variation, équation, théorème des valeurs intermédiaires, tableau de signe.
Exercice N°243 :
Exercice N°243 :
Soit f la fonction rationnelle définie sur Df = ]-∞ ; 2[ ⋃ ]2 ; +∞[
par
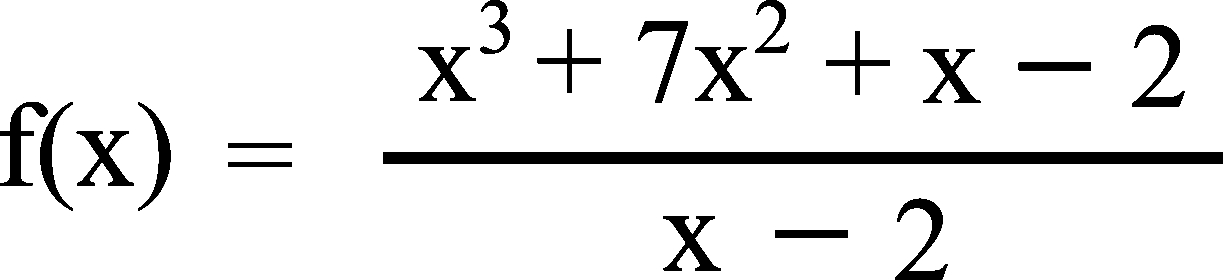
1) Étudier les limites aux bornes du domaine de définition Df et donner ses asymptotes éventuelles. Lis la suite »
Exercice de maths de terminale sur le bac 2016 sur la fonction, intégrale, primitive, logarithme népérien, dérivée, variation, TVI, surface.
Exercice N°600 :
Exercice N°600 :
La courbe (C) ci-dessous représente, dans un repère orthonormé, une fonction f définie et dérivable sur [0.5 ; 6]. Les points A(1 ; 3) et B d’abscisse 1,5 sont sur la courbe (C).
Les tangentes à la courbe (C) aux points A et B sont aussi représentées en pointillés sur ce graphique, la tangente au point B est horizontale.
On note f ‘ la fonction dérivée de f.
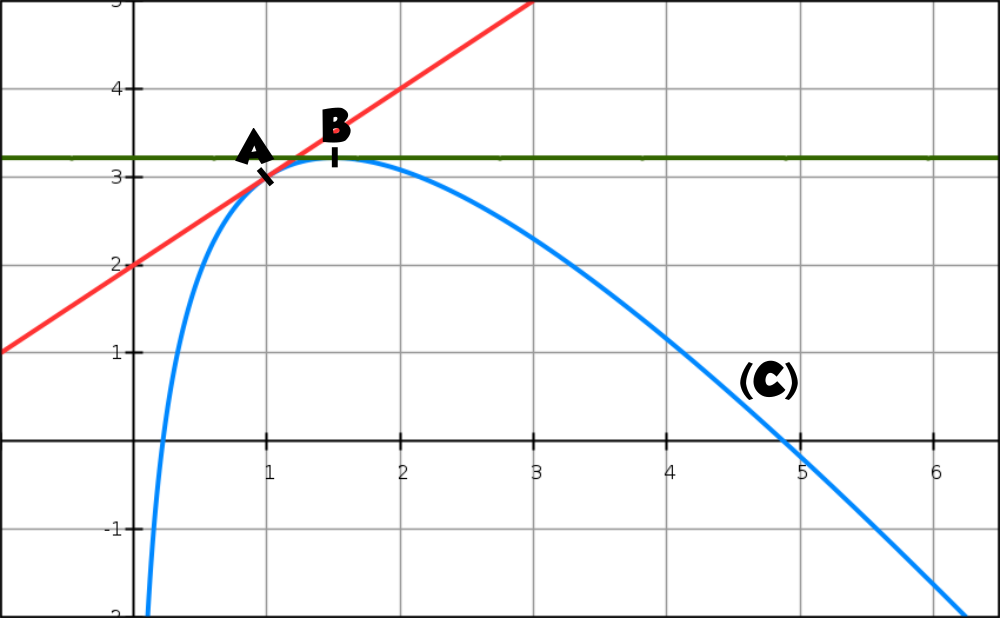
Les parties A et B sont indépendantes.
Partie A : Étude graphique
1) Déterminer f ‘ (1,5). Lis la suite »
Exponentielle – Continuité, équation, tableau, variation – Terminale
5 septembre 2021
Maths de terminale : exercice d’exponentielle avec continuité et équation. Tableau de variation, solution unique, encadrement.
Exercice N°750 :
Exercice N°750 :
On considère la fonction f définie sur R par
f(x) = (-4x2 + 5)e-x + 3.
On note (C) la courbe représentative de la fonction f dans un repère orthogonal.
On note f ‘ la dérivée de f sur R.
1) Démontrer que pour tout réel x ∈ R,
f ‘ (x) = (4x2 – 8x – 5)e-x. Lis la suite »
Exponentielle – Continuité, équation, solution unique – Terminale
5 septembre 2021
Maths de terminale : exercice d’exponentielle avec variation et continuité, équation avec solution unique, coût de production, primitive.
Exercice N°749 :
Exercice N°749 :
Soit f la fonction définie sur [0 ; 5] par
f(x) = (ax + b)e−x
où a et b sont deux réels.
On note f ‘ la fonction dérivée de f.
1) Montrer que pour tout nombre réel x,
f ‘ (x) = (a − b − ax)e−x. Lis la suite »
