Maths de terminale : exercice, fonction, continuité, limite, variation, équation, théorème des valeurs intermédiaires, tableau de signe.
Exercice N°243 :

Exercice N°243 :
Soit f la fonction rationnelle définie sur Df = ]-∞ ; 2[ ⋃ ]2 ; +∞[
par
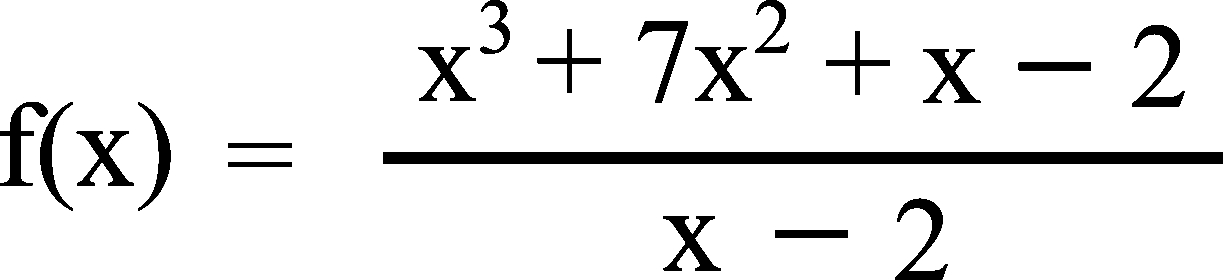
1) Étudier les limites aux bornes du domaine de définition Df et donner ses asymptotes éventuelles.
2) Prouver que f est dérivable sur ]-∞ ; 2[ et ]2 ; +∞[, puis vérifier que
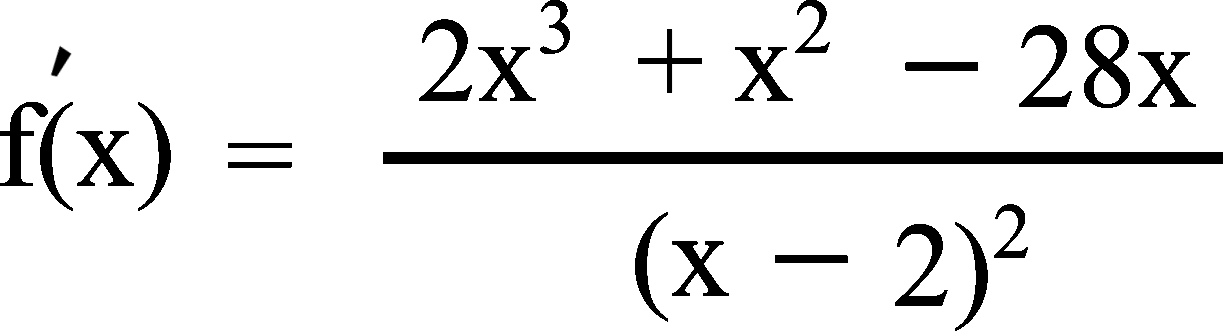
3) Étudier le signe du trinôme
t(x) = 2x2 + x – 28
suivant les valeurs de x appartenant à R.
4) En déduire le tableau de signe de f ‘ (x).
5) Construire le tableau de variations de f.
6) Justifier que l’équation f(x) = 0 admet une solution unique α dans l’intervalle [-4 ; 0].
7) Donner un encadrement de α de largeur 10-2.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, fonction, continuité, limite.
Exercice précédent : Dérivation – Cosinus, racine, exponentiel, rationnelle – Terminale

