Exercice de maths sur la fonction exponentielle, suite, récurrence, terminale, continuité, équations, convergence, raisonnement, variations.
Exercice N°284 :

Exercice N°284 :
Le but de l’exercice est de démontrer que l’équation (E) ∶
xex = 1
admet une unique solution dans l’ensemble R des nombres réels, et de construire une suite qui converge vers cette unique solution.
Existence et unicité de la solution :
On note f la fonction définie sur R par
f(x) = x − e−x.
1) Démontrer que x est solution de l’équation (E)
si et seulement si f(x) = 0.
2) Étudier le sens de variation de la fonction f sur R.
3) En déduire que l’équation (E) possède une unique solution sur R, notée α.
4) Justifier que α appartient à l’intervalle [1/2 ; 1].
5) Étudier le signe de f sur l’intervalle [0 ; α].
Deuxième approche :
On note g la fonction définie sur l’intervalle [0 ; 1] par
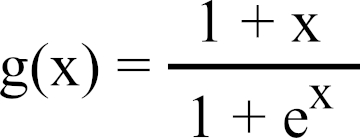 .
.
6) Démontrer que l’équation f(x) = 0 est équivalente à l’équation
g(x) = x.
7) En déduire que α est l’unique réel vérifiant g(x) = x.
8) Calculer g ‘ (x) et en déduire que la fonction g est croissante sur [0 ; α].
Construction d’une suite de réels ayant pour limite α :
On considère la suite (un)n∈N définie par
u0 = 0 et,
pour tout entier naturel n, un+1 = g(un).
9) Démontrer par récurrence que, pour tout entier naturel n :
0 ≤ un ≤ un+1 ≤ α
10) En déduire que la suite (un) est convergente. On note l sa limite.
11) Justifier l’égalité g(l) = l et en déduire la valeur de l.
12) A l’aide de la calculatrice, déterminer une valeur approchée de u4 arrondie à la sixième décimale.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exponentielle, suite, récurrence, terminale.
Exercice précédent : Exponentielle – Fonctions, suite, continuité, limite – Terminale

