Exercice de maths de première : position relative de parabole et de droite. Inéquations équations, second degré, intersections, coordonnée.
Exercice N°259 :
Exercice N°259 :
1) Résoudre cette première inéquation sur R :
Exponentielle – Equation, dérivée, limite, variation – Terminale
12 octobre 2022
Maths : exercice sur dérivée et exponentielle de terminale. Équations, inéquations, dérivées, limites, tableau de variations, asymptotes.
Exercice N°275 :
Exercice N°275 :
1-6) Résoudre les équations suivantes :
1) ex = -4, Lis la suite »
Maths de première : exercice de trigonométrie avec polynôme, troisième degré, équations, sinus, cosinus, intervalle, factorisation, formule.
Exercice N°803 :
Exercice N°803 :
Polynôme et trigonométrie :
1) Factoriser le polynôme :
P(x) = 4x3 – 2x2 – 3x + 1. Lis la suite »
Maths de première : exercice de trigonométrie avec formules d’angles associés, sinus, cosinus, valeurs exactes, cercle trigonométrique.
Exercice N°802 :
Exercice N°802 :
1-2-3-4) On donne cos x = –1/3 et x ∈ [0 ; π].
1) Calculer sin(x) en détaillant les étapes. Lis la suite »
Maths de première : exercice de trigonométrie avec sinus et cosinus. Fonction, tableau de variation, valeurs, équations, majorant, minorant.
Exercice N°801 :
Exercice N°801 :
1) x désigne un nombre réel tel que 0 < x < π/2.
On a cos x = ( √( √2 + 2 ) )/2.
Calculer cos(2x) et en déduire x. Lis la suite »
Maths de première : exercice de problèmes du second degré. Énoncé, situation, mise en équation, résolution, trouver les solutions.
Exercice N°800 :
Exercice N°800 :
Pour chaque situation, trouver l’équation du second degré adéquate et la résoudre pour répondre à la question posée.
1) Plusieurs personnes se sont réunies pour fêter Noël. Chaque personne a apporté 3 cadeaux à chacune des autres personnes. Sachant qu’au total 468 cadeaux ont été déposés près de l’arbre de Noël, combien de personnes y avait-il?. Lis la suite »
Maths de première : exercice pour trouver les coefficients d’un polynôme du troisième degré. Courbe, dérivation, équations, système.
Exercice N°797 :
Exercice N°797 :
Afin d’éviter le passage en centre-ville d’une ligne TGV, on effectue un changement du tracé de cette ligne. Sur le plan ci-dessous, G
représente l’ancienne gare et C la nouvelle gare desservant la ville.
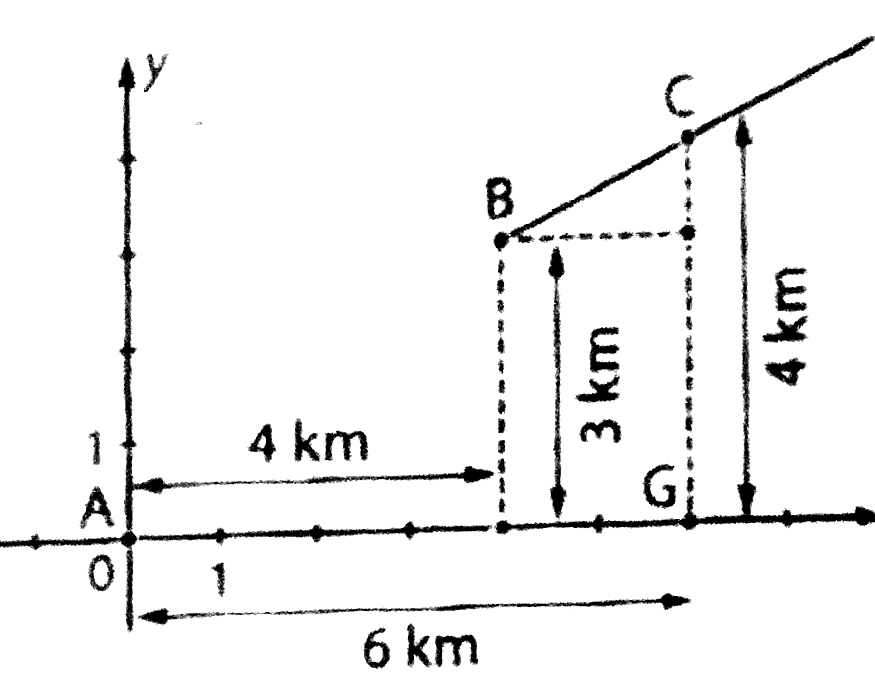
On se propose de raccorder des deux tronçons rectilignes, c’est-à-dire la partie de l’axe des abscisses à gauche de A et la demi-droite [BC], par une courbe plane.
Le raccordement doit être tangent à ces deux tronçons rectilignes.
On modélise le problème du traçé à l’aide d’une fonction f définie sur R de la forme :
f(x) = ax3 + bx2 + cx + d
avec a, b, c et d quatre coefficients réels.
Le raccordement se fait entre les points A et B. On choisit un repère d’origine A comme c’est indiqué sur le schéma. L’axe des abscisses est la droite (AG).
1) Justifier que f(0) = 0 et que f ‘(0) = 0. Lis la suite »
Maths de première : exercice d’exponentielle avec équations et variation. Fonction, inéquations, calculs de dérivées, tableau de signe.
Exercice N°660 :
Exercice N°660 :
1-6) Résoudre les équations suivantes :
1) ex = -4 Lis la suite »
Maths de seconde sur les fonctions affines. Exercice de droite, point d’intersection, sécantes, système d’équation, fraction, inconnues.
Exercice N°622 :
Exercice N°622 :
Soit (d1) la droite d’équation
y = -2 x + 1,
et (d21) la droite d’équation
y = (1/2)x + 1.
1) Faire une figure (tracer les deux droites et placer les points). Lis la suite »
Exercice de maths de seconde sur système d’équation et second degré. Coefficient de polynôme, points, courbe, calculs de variables.
Exercice N°620 :
Exercice N°620 :
On considère la fonction f définie par
f(x) = x2 + ax + b
où a et b sont des nombres réels que l’on cherche à déterminer. On souhaite que la courbe représentative Cf de cette fonction f, passe par
les points A(−1 ; 6) et B(1 ; 2).
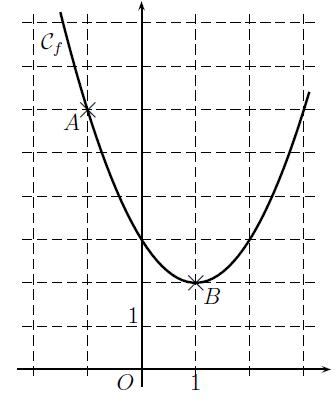
1) Déterminer les réels a et b et donner l’expression de la fonction f vérifiant ces deux conditions. Lis la suite »
