Exercice de maths avec algorithme, terminale, conjecturer, suite. Repère, graphique, auxiliaire géométrique, premier terme, raison, limite.
Exercice N°212 :

Exercice N°212 :
On donne ci-dessous la représentation graphique des 16 premiers termes d’une suite (un) dans le plan muni d’un repère orthogonal.
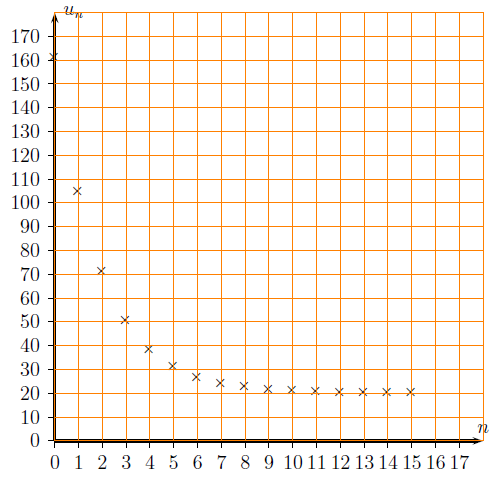
1) Conjecturer la limite de la suite (un).
Les quatre premiers termes de la suite (un) ont été calculé avec un tableur :
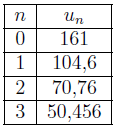
2) La suite (un) peut-elle être une suite géométrique ? Justifier.
3) La suite (un) observée dans la partie A est définie pour tout entier naturel n par
un+1 = 0.6un + 8
et
u0 = 161.
Calculer u4.
4) Soit (vn) la suite définie pour tout entier naturel n par
vn = un − 20.
Montrer que (vn) est une suite géométrique. On précisera le premier terme et la raison.
5) Donner l’expression de vn en fonction de n, puis l’expression de un en fonction de n.
6) Déterminer la limite de la suite (vn) et en déduire celle de la suite (un).
7) Écrire en langage naturel l’algorithme d’un programme qui demande à l’utilisateur de saisir un entier naturel n et affiche en résultat le nombre un.
8) Transcrire l’algorithme précédent dans le langage de programmation Python.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : algorithme, terminale, conjecturer, suite.
Exercice précédent : Suites – Récurrent, géométrique, explicite, limite- Terminale

