Maths de terminale : exercice de convexité avec point d’inflexion. Fonction polynôme, sa courbe, variations , équation de tangente.
Exercice N°309 :
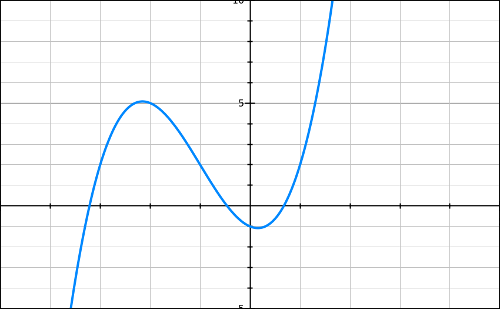
On considère la fonction f définie sur [-3 ; 1.5] par l’expression
f(x) = x3 + 3x2 – x – 1.
Cette fonction est représentée ci-dessus.
1) Étudier les variations de la fonction f.
2) Donner l’équation de la tangente T-2 à la courbe Cf au point d’abscisse -2. Tracer avec précision cette tangente.
3) En quel(s) point(s) la courbe admet-elle une tangente horizontale ? Justifier.
4) Calculer f ‘ ‘ (x) puis étudier la convexité de la fonction.
5) La courbe Cf admet elle un(des) point(s) d’inflexion ? Justifier.
6) Le cas échéant, donner l’équation de la tangente au(x) point(s) d’inflexion et tracer avec précision la tangente.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, convexité, point inflexion.
Exercice précédent : Convexité – Fonction, variations, solution unique – Terminale

