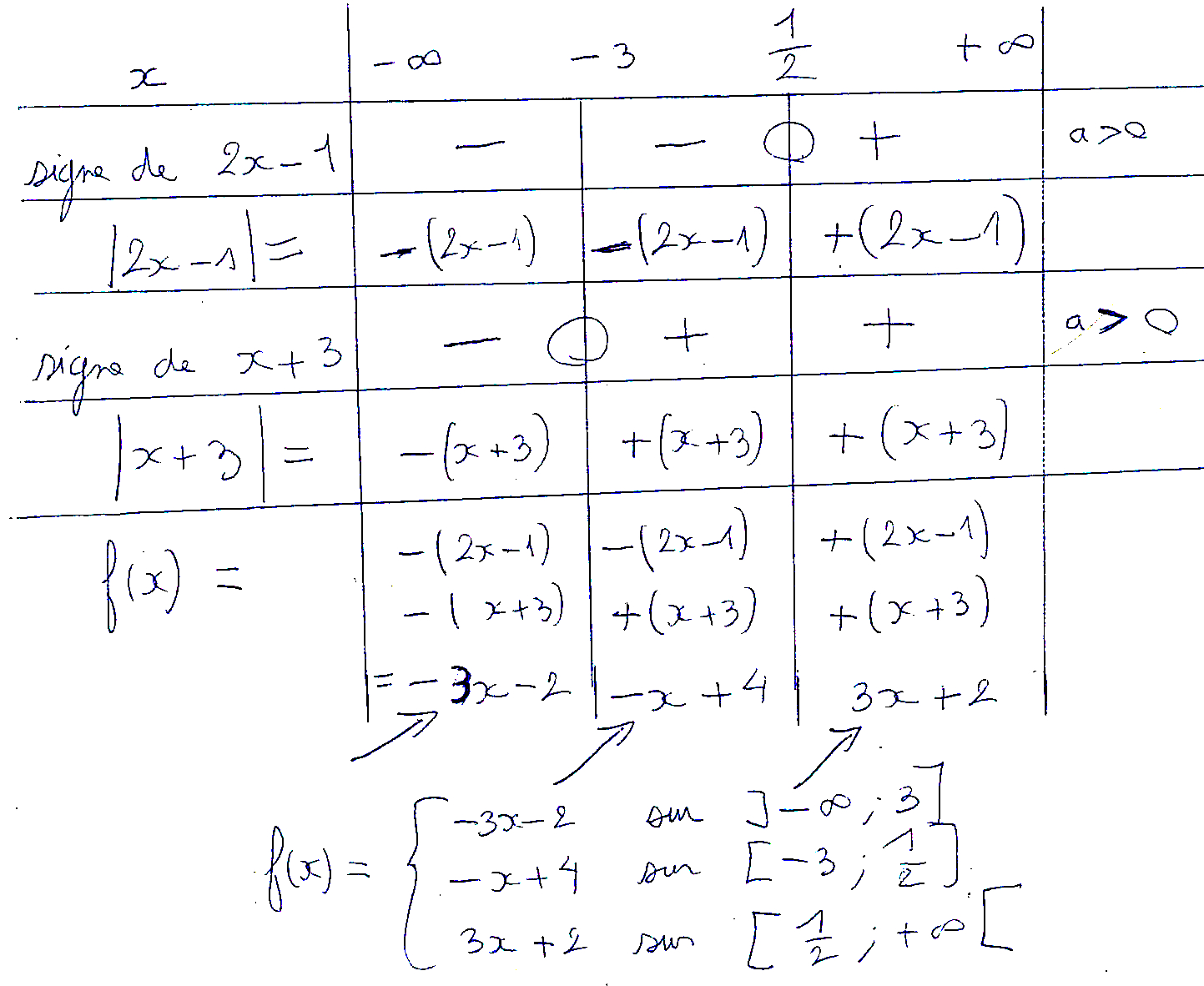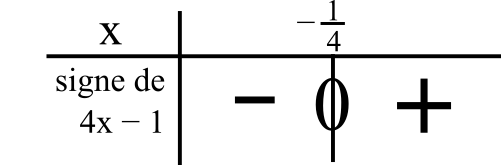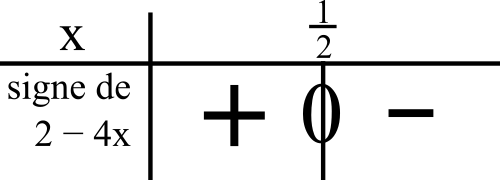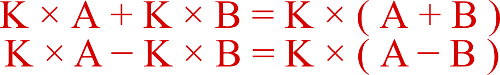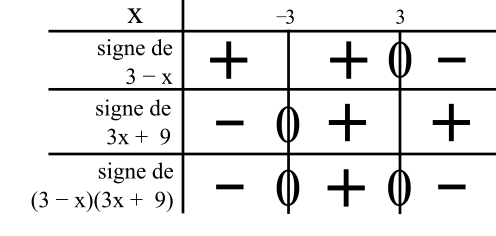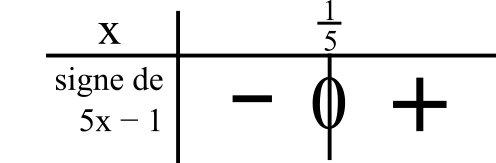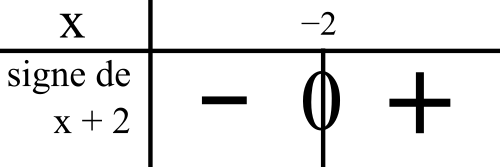frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Voici le dessin de la pyramide :

I est le milieu de [SB], J est le milieu de [SC]. D’après le théorème de la droite des milieux, (IJ) // (BC).
On sait aussi que ABCD est un parallélogramme
donc (AD) // (BC).
Or, deux droites parallèles à une même troisième droite (ici (BC)) sont parallèles entres elles, donc (IJ) // (AD).

2) Voici le dessin du plan (SDK) :

Comme (IJ) est parallèle à (AD), alors (IJ) est parallèle à tout plan contenant (AD) comme (SDA). Donc (IJ) // (SDA).

Or (SDA) et (SDK) sont sécants en (SD) car cette droite est commune aux deux plans et ils ne sont pas confondus.
Il est clair que (SD) n’est pas parallèle à (IJ) car (IJ)//(AD).

Raisonnement par l’absurde :
On sait que (IJ) // (SDA) et on suppose (IJ) // (SDK).
Si une droite est parallèle à deux plans et,
si ces deux plans sont sécants,
alors leur intersection (ici (SD)) est une droite parallèle à la droite en question (ici (IJ)) :
soit (IJ) // (SD).
Or on n’a vu plus haut que ce n’est pas le cas : donc (IJ) ne peut pas être parallèle à (SDK).

Donc (SDK) et (IJ) sont sécants.

3) L’intersection de deux plans sécants est une droite. Il faut donc trouver deux points qui sont à la fois sur (SDK) et (SBC). On a déjà le point S d’après de le nom des plans.

Quand on regarde la figure, on voit que (DK) et (BC) sont sur un même plan, celui du « sol ».
La droite (DK) appartient au plan (SDK) et la droite (BC) appartient au plan (SBC) d’après les noms.
De plus, (DK) et (BC) sont sécantes : elles ont donc un point d’intersection qui appartient aux deux droites. Du coup, ce point d’intersection appartient aux deux plans (SDK) et (SBC).
Pour le tracer, il suffit de prolonger les droites assez loin.

Voici le dessin du prolongement des droites et du point d’intersection :

Avec ces deux points (S et ce dernier), on a la droite d’intersection. Il suffit de la tracer.

4) On sait que (IJ) et (SKD) sont sécant d’après la question 1).

On connait l’intersection du plan (SBC) avec (SDK). C’est la droite rouge.
Or la droite (IJ) appartient à la face -au plan- (SBC), donc son intersection avec (SKD) sera sur la droite rouge.

Voici le dessin de la droite rouge et du point d’intersection de (IJ) et (SDK) :

Je justifie ci-dessous :

L’intersection de deux droites sécantes est un point. En prolongeant (IJ) vers la droite rouge, on trouve le point d’intersection (en noir) de (IJ) et de cette droite, soit l’intersection de (IJ) et de (SKD).

Exercice : Clic droit sur l’exercice

Tout le corrigé :

Quand on calcule un éventuel nombre dérivé f ‘ (a) en x = a, on cherche à trouver ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} en fonction de h.
Puis on tend ce h vers 0 pour arriver à une limite.
Si tu trouves une constante, tu obtiens que la fonction est dérivable en x = a et que ce nombre est f ‘ (a).

1)

Donc le taux de variation ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} admet une limite finie en a = 2 donc le nombre f ‘ (2) existe et vaut -1.
Donc f est dérivable en 2 et f ‘ (2) = -1.

Donc le coefficient de la tangente à Cf en a = 2 est égal à -1.

2)

J’ai oublié le « h » devant la flèche « →0 ».

Donc le taux de variation ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} admet une limite finie en a = 4 donc le nombre f ‘ (4) existe et vaut ¹/₂.
Donc f est dérivable en 4 et f ‘ (4) = ¹/₂.

Donc le coefficient de la tangente à Cf en a = 4 est égal à ¹/₂.

3)

J’ai oublié le « h » devant la flèche « →0 ».

Donc le taux de variation ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} admet une limite finie en a = 3 donc le nombre f ‘ (3) existe et vaut –¹/₃.
Donc f est dérivable en 3 et f ‘ (3) = –¹/₃.

Donc le coefficient de la tangente à Cf en a = 3 est égal à –¹/₃. Comme notre fonction est affine, la tangente est la droite elle-même.

4) En a = -2, on a x + 2 = 0, donc le contenu de la valeur absolue est nul.
Or la fonction « valeur absolue » n’est pas dérivable en 0.
Donc la valeur absolue de x + 2 n’est pas dérivable en -2.
Il n’y a donc pas de nombre dérivé de |x + 2| en a = -2.

A gauche, on voit la courbe de la fonction représentant |x + 2|.
A droite, celle de |x].
En a = -2, sur la courbe de gauche, on est sur la « pointe » des deux demi-droites, il n’y a pas de tangente qui suit la courbe en a = -2.

Bonne compréhension,
laisse un commentaire en cas de problème,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) On voit sur le graphique que f(0) = 2.
On peut remplacer x par 0 dans la fonction. Et cela donnera 2.
f(0) = a×0³ + b×0² + c×0 + d = 2 soit d = 2.

La courbe admet une tangente horizontale au point d’abscisse 0 (car parallèle à l’axe des abscisses), sa pente est donc de 0, donc f ‘ (0) = 0.

La dérivée de ax³ + bx² + cx + 2 est
f ‘ (x) = 3ax² + 2bx + c.
Donc f ‘ (0) = 3a×0² + 2b×0 + c = 0.
Soit c = 0.

On obtient donc f(x) = ax³ + bx² + 2.

2) f(3) = 0
soit a×3³ + b×3² + 2 = 0
soit 27a + 9b + 2 = 0.
Cela nous donne une égalité pour l’instant.

f ‘ (3) = 0 car la courbe admet une tangente horizontale en B d’abscisse x = 3 (parallèle à l’axe des abscisses).

Du coup, en reprenant l’expression de f ‘ (x) plus haut,
f ‘ (3) = 3a×3² + 2b×3 + c = 0.
Soit 27a + 6b + 0 = 0 qui est une seconde égalité.

Nous obtenons un système avec les deux égalités :
{ 27a + 9b + 2 = 0
{ 27a + 6b = 0
soit (comme nous avons 27a et 27a, isolons les) :
{ 27a = -9b – 2
{ 27a = -6b
soit (27a = 27a donc les membres de droite sont égaux)
{ -9b – 2 = -6b
{ 27a = -6b (je conserve l’une des deux lignes)

On résout séparément :
-9b – 2 = -6b
soit -9b + 6b = 2
soit -3b = 2
soit b = –²/₃.

Reprenons le système équivalent au précédent système avec la valeur de b :
{ b = –²/₃
{ 27a = -6b

soit
{ b = –²/₃
{ 27a = -6*(-²/₃)

soit
{ b = –²/₃
{ 27a = +¹²/₃

soit
{ b = –²/₃
{ 27a = 4

soit
{ b = –²/₃
{ a = ⁴/₂₇.

Donc f(x) = (⁴/₂₇)×x³ – (²/₃)×x² + 2.

3) f(1) = (⁴/₂₇)×1³ – (²/₃)×1² + 2
= (⁴/₂₇) – (2/3) + 2
= ⁴/₂₇ – ¹⁸/₂₇ + ⁵⁴/₂₇
= ⁴⁰/₂₇.

Le point d’abscisse 1 de la courbe a pour coordonnées
(1 ; f(1)) soit (1 ; ⁴⁰/₂₇).

4) Le coefficient d’une tangente en un point d’une courbe est f ‘(a) avec a l’abscisse du point.
En reprenant f ‘ (x) = 3ax² + 2bx + c
= 3×(⁴/₂₇)x² + 2×(-²/₃)x + 0
= (⁴/₉)x² – (⁴/₃)x.

f ‘ (1) = ⁴/₉ – ⁴/₃
= ⁴/₉ – ¹²/₉
= –⁸/₉.

Le coefficient directeur de cette tangente est donc –⁸/₉.

Bonne compréhension,
Sylvain

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) L’aire du triangle AEF est égale à la moitié de l’aire du triangle ABC.

Cela revient à :
Aire_AEF = (¹/₂) × Aire_ABC

Les triangles sont rectangles en A donc le Base × Hauteur × (¹/₂) devient :
Côté1 × Côté2 × (¹/₂) en prenant les deux côtés auprès de l’angle droit.

AF × AE × (¹/₂) = (¹/₂) × AC × AB × (¹/₂)
⇔ AF × AE = (¹/₂) × AC × AB (en multipliant par 2 de chaque côté du « = »).
⇔ x × (18 – x) = (¹/₂) × 8 × 18
⇔ -x² + 18x – 72 = 0.

Nous avons une équation du second degré, calculer le discriminant est utile :
Δ = 18² – 4 × (-1) × (-72)
= 324 – 288 = 36 > 0.

x1 = ^{(-b – √Δ)}/_2a
= ^{(-18 – √36)}/_-2
= ^{(-18 – 6)}/_-2
= ^(-24)/_-2 = 12.

x2 = ^{(-18 + 6)}/_-2
= ^(-12)/_-2 = 6.

x ne peut pas être égal à 12 car il ne peut pas dépasser AC = 8 car F ne peut pas aller au-dessus de C.
Donc x = 6.

2) 2x² + 9x − 5 :

La forme canonique d’une fonction polynôme s’écrit :
a(x – x_Sommet)² + y_Sommet

x_Sommet = ^-b/_2a
= ^-9/₄

y_Sommet = ^-Δ/_4a
= ^{-(81 – 4*2*(-5))}/₈
= ^-(121)/₈

Donc f(x) = 2(x – (^-9/₄))² + (^-121/₈).

3) Comme un carré est toujours positif ou nul,

2(x – (^-9/₄))² l’est toujours car le facteur 2 est aussi positif donc produit positif.
Donc f(x) est toujours plus grand ou égal à ^-121/₈.

4) −2x² − 16x − 32 = 0 :

Il n’y a que des « moins » donc je multiplie tout par (-1).
2x² + 16x + 32 = 0

Je calcule le discriminant Δ car nous avons affaire à un polynôme du second degré.
Δ = b² – 4ac
= 16 × 16 – 4 × 2 × 32
= 256 – 256 = 0.

On a donc une racine double x₁
= ^-b/_2a
= ^-16/₄ = -4.

et x₂ = ^-b/_2a
= -4 aussi.

S = {-4}.

5) ⁴/_{(x − 1)} − ³/_{(x − 2)} = −1 :

On a une égalité avec des fractions, on passe tout à gauche et on met au même dénominateur.
⁴/_{(x − 1)} − ³/_{(x − 2)} + 1 = 0

Je choisis (x-1)(x-2) comme dénominateur.

⇔ ^{4(x – 2)}/_{(x − 1)(x − 2)} − ^{3(x – 1)}/_{(x − 1)(x − 2)} + ^{(x − 1)(x − 2)}/_{(x − 1)(x − 2)} = 0

⇔ ^{[ 4(x – 2) − 3(x – 1) + (x − 1)(x − 2) ]}/_{(x − 1)(x − 2)} = 0

Une fraction est nulle si et seulement si son numérateur est nul. On obtient donc :
4(x – 2) − 3(x – 1) + (x − 1)(x − 2) = 0
⇔ 4x – 8 -[3x – 3] + x² – 2x – x + 2 = 0
⇔ 4x – 8 – 3x + 3 + x² – 3x + 2 = 0
⇔ x² – 2x – 3 = 0

On calcule le discriminant :

Δ = b² – 4ac = (-2) × (-2) – 4 × 1 × (-3)
= 4 + 12 = 16 > 0.
Deux racines, c’est à dire x₁ et x₂ qui font que le trinôme fait 0, soit deux solutions ici.

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-(-2) – √16)}/₂
= ^{(2 – 4)}/₂
= ^(-2)/₂
= -1.

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-(-2) + √16)}/₂
= ^{(2 + 4)}/₂
= ⁶/₂
= 3.

On obtient S = {-1 ; 3}.

6) 6x² − 13x + 6 > 0 :

Pour résoudre une inéquation avec 0 à droite, il faut faire un tableau de signe.
Là, on a un polynôme du second degré donc je fais Delta.

Δ = b² – 4ac = (-13) × (-13) – 4 × 6 × 6
= 169 – 144 = 25 > 0.

On obtient deux racines, c’est à dire x1 et x2 qui font que le trinôme fait 0.

x1 = ^{(-b – √Δ)}/_(2a)
= ^{(13 – √25)}/₁₂
= ^{(13 – 5)}/₁₂
= ⁽⁸⁾/₁₂
= ²/₃,

x2 = ^{(13 + 5)}/₁₂
= ⁽¹⁸⁾/₁₂
= ³/₂.

On se retrouve avec un tableau de signe avec les racines ²/₃ puis ³/₂ :
x : -∞ ²/₃ ³/₂ +∞
Les zéros sont en dessous des deux racines et comme le signe de a est positif (6), le signe de a étant à l’extérieur des racines,
on obtient le tableau de signe de 6x² − 13x + 6 : + 0 – 0 + c’est-à-dire d’abord positif, puis zéro, puis négatif, puis zéro, puis positif.

Comme on veut que le trinôme soit > 0, on ne garde que les + soit :
S = ]-∞ ; ²/₃[ U ]³/₂ ; +∞[.

7) Pour résoudre une inégalité avec 0 à droite,

on doit faire un tableau de signe. On gardera les 0 car l’égalité est large. Et on veut des « moins ».

On calcule le discriminant :
Δ = 2 × 2 – 4 × (-3) × (-1) = 4 – 12 = -8 < 0.

Comme Δ est strictement négatif, il n’y a pas de racine et le trinôme est toujours du signe de a (soit -3) donc il est négatif.

Dans le tableau de signe de −3x² + 2x − 1, on met un grand « moins » de -∞ à +∞.
Donc S = R car la question demande que ce trinôme soit inférieur ou égal à zéro et c’est toujours le cas.

Exercice : Clic droit vers l’exercice

Tout le corrigé :

Dans cet exercice de variation, on ne passera pas par la dérivation car en général, les élèves n’ont pas vu ce chapitre à ce moment là.

Cours :

Pour étudier les variations de f, on doit prendre a < b et comparer f(a) et f(b).

Si on a f(a) < f(b), la fonction est strictement croissante (on garde le « <« ).

Si on a f(a) ≤ f(b), la fonction est juste croissante (on garde le sens de l’inégalité).

Si on a f(a) > f(b), la fonction est strictement décroissante (on passe à « > »).

Si on a f(a) ≥ f(b), la fonction est strictement décroissante (on change le sens de l’inégalité).

Corrigé des questions :

1) Sur I = [-7 ; -1] avec
u(x) = ¹/_x
et
v(x) = ^-8/_x.

Une fonction de type fraction est définie quand son dénominateur est différent de 0. Ici le dénominateur est « x » et il doit être différent de 0. Donc c’est bon sur I = [-7 ; -1].

Partons de a < b :

On a donc -1 ≤ a < b ≤ -7

En passant à l’inverse :

¹/_(-1) ≥ ¹/_a > ¹/_b ≥ ¹/_(-7)

Le sens de l’inégalité change car la fonction « inverse » est strictement décroissante.

On obtient u(a) > u(b).

Pour tout a et b de l’intervalle I, a < b donne u(a) > u(b),
donc la fonction u est strictement décroissante.

Pour v, on reprend l’inégalité précédente :

-1 ≥ ¹/_a > ¹/_b ≥ –¹/₇
+8 ≤ ^(-8)/_a < ^(-8)/_b ≤ +⁸/₇

On obtient v(a) < v(b).

Pour tout a et b de l’intervalle I, a < b donne v(a) < v(b),
donc la fonction v est strictement croissante.

2) Sur I =]-1 ; 0] avec
u(x) = -2x + 5
et
v(x) = √(-2x + 5).

u est une fonction affine dont le coefficient directeur -2 est négatif. Donc u est décroissante.

v est du type racine, il faut donc que l’intérieur soit positif ou nul. Du coup, on fait le tableau de signe du contenu -2x + 5.

-2x + 5 ≥ 0
⇔ -2x ≥ -5
⇔ x ≤ ⁵/₂
(on change le sens des inégalités car on divise par le nombre négatif -2)

Comme a = -2 < 0, la courbe descend, donc la fonction u est d’abord positive puis négative. Donc elle est positive avant 2,5. Comme son contenu est positif, la racine existe donc pour x appartenant à ]-1 ; 0] donc la fonciton v est bien définie.

Pour tout a et b tels que -1 ≤ a < b ≤ 0 :

On a u(-1) ≥ u(a) > u(b) ≥ u(0)
(Changement du sens des inégalités car u est décroissante)

√u(-1) ≥ √u(a) > √u(b) ≥ √u(0)
car la fonction « racine » est strictement croissante pour les réels positifs ou nuls donc on ne change pas le sens des inégalités.

v(-1) ≥ v(a) > v(b) ≥ v(0)

Pour tout a et b de l’intervalle I, a < b donne v(a) > v(b),
donc la fonction v est strictement décroissante (car le sens de l’inégalité a changé)).

3) I = [-5 ; -2] avec
u(x) = x^² – 2
et
v(x) = ¹/_{(x^² – 2)}.

u est une fonction polynôme donc définie sur R.

Comme on divise par u(x) pour obtenir la fraction v(x), il faut que u(x) soit différent de 0 sur l’intervalle [-5 ; -2].

Pour cela, on fait un Δ = b² – 4ac = 8,
x1 = -√2 (environ égal à 1,41).
et x2 = √2 (environ égal à -1,41).
On voit que ces racines ne sont pas dans l’intervalle [-5 ; -2].

Comme on ne divise pas par 0, v est bien définie sur I = [-5 ; -2].

Pour la variation, on prend a et b appartenant à I tel que a < b :

On part de : -5 ≤ a < b ≤ -2

(-5)² ≥ a² > b² ≥ (-2)²
(on change les sens car la fonction « carré » est décroissante sur ]-∞ ; 0]).

25 – 2 ≥ a² – 2 > b² – 2 ≥ 2

A partir de a < b, on obtient donc au milieu u(a) > u(b)
donc u est strictement décroissante sur I car le sens de l’inégalité a changé.

Comme on doit passer par l’inverse pour obtenir v, v devient strictement croissante car « inverse » change le sens de variation (La fonction « inverse » est décroissante).

4) f(x) = |2x – 1| + |x + 3| :

Avec des valeurs absolues, la première chose à faire, c’est d’étudier le signe du contenu des valeurs absolues entre les « | » »| ».

Si A ≥ 0, |A| = A.
Si A < 0, |A| = -A.

D’une part :

2x – 1 ≥ 0
⇔ x ≥ ¹/₂.

Donc le tableau de signe est dans le sens – 0 + car a = 2 > 0.

Du coup, |2x – 1| s’écrit d’abord -(2x-1) car le contenu est négatif pour les x inférieurs à ¹/₂.
Puis |2x – 1| s’écrit ensuite 2x-1 car le contenu est positif pour les x supérieurs à ¹/₂.

D’autre part :

x + 3 ≥ 0
⇔ x ≥ -3.

Donc le tableau de signe est dans le sens – 0 + car a = 1 > 0.
Du coup, |x + 3| s’écrit d’abord -(x+3) car le contenu est négatif pour les x inférieurs à -3.
Puis |x+3| s’écrit ensuite x+3 car le contenu est positif pour les x supérieurs à 3.

5) Pour résoudre f(x) = 4, on résout sur chaque intervalle :

-3x – 2 = 4 sur ]-∞ ; -3 ]
⇔ -3x = 6
⇔ x = -2
et on sort de l’intervalle ]-∞ ; -3 ] donc cette valeur ne convient pas.

-x + 4 = 4 sur ] -3 ; ¹/₂ ]
⇔ -x = 0
⇔ x = 0
que l’on conserve car on est bien dans l’intervalle ] -3 ; ¹/₂ ].

3x + 2 = 4 sur ] ¹/₂ ; +∞ [
⇔ 3x = 2
⇔ x = ²/₃
que l’on conserve car on est bien dans l’intervalle ] ¹/₂ ; +∞ [.

On obtient donc S = { 0 ; ²/₃ }.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) (5x – 1)(2 – 3x) ≥ 0 :

Rédaction :

Pour résoudre une inéquation avec ≥ 0, l’idéal est de construire le tableau de signe de l’expression de gauche et de déterminer les intervalles de x où il y a les « + » et « 0 ».

Pour cela, on doit d’abord obtenir les signes de 5x – 1
et de 2 – 3x séparément. J’effectue des petites inéquations que j’appelle mini-inéquations.

On a le signe « + »
quand 5x – 1 ≥ 0
quand 5x ≥ 1
quand ^5x/₅ ≥ ¹/₅
(on garde le sens de l’inégalité car on divise par un nombre positif de chaque côté)
quand x ≥ ¹/₅
Cela veut dire que c’est à droite de ¹/₅ dans le tableau.

On mettra donc le signe « + » à droite de ¹/₅.

On a le signe « + »
quand 2 – 3x ≥ 0
quand -3x ≥ -2
quand ^-3x/_-3 ≤ ^-2/_-3
(on change le sens de l’inégalité car on divise par un nombre négatif de chaque côté)
quand x ≤ ²/₃
Cela veut dire que c’est à gauche de ²/₃ dans le tableau.

On mettra donc le signe « + » à gauche de ²/₃.

Voici le tableau de signe :

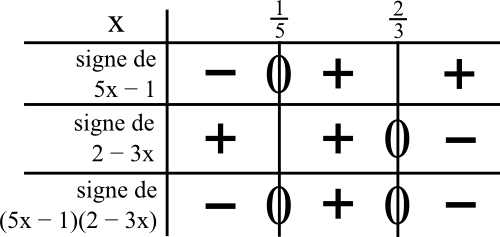
Comme on veut (5x – 1)(2 – 3x) ≥ 0, on prend les « + » et les « 0 » dans le tableau, soit des crochets fermés. L’intervalle des solutions est donc :
S = [¹/₅ ; ²/₃].

2) [³/_{(4x + 1)}] – 1 > 0 :

Rédaction :

Attention, il y a une fraction avec des x, c’est-à-dire, une fonction rationnelle. Il faut donc déterminer l’ensemble de définition de l’équation.

Or une fonction rationnelle est définie si et seulement si son dénominateur est différent de zéro.
On va donc faire le tableau de signe du dénominateur et exclure les valeurs de x qui font que ce dénominateur est égal à zéro.

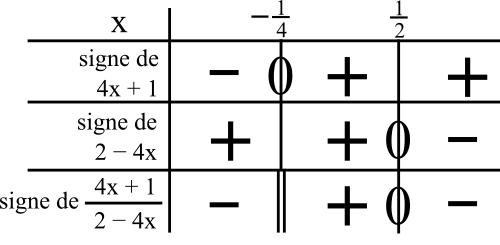
On a le signe « + »
quand 4x + 1 ≥ 0
quand 4x ≥ -1
quand ^4x/₄ ≥ –¹/₄
(on garde le sens de l’inégalité car on divise par un nombre positif de chaque côté)
quand x ≥ –¹/₄
Cela veut dire que c’est à droite de –¹/₄ dans le tableau.

On mettra donc le signe « + » à droite de –¹/₄.

Le dénominateur est donc nul quand x = –¹/₄.
Le domaine de définition de l’inéquation est donc R privé de –¹/₄.

Donc :

Pour résoudre une inéquation avec 0 à droite, il faut faire un tableau de signe de l’expression de gauche.

[³/_{(4x + 1)}] – 1 > 0

Pour résoudre cette inéquation avec une fraction et une soustraction, l’astuce est de tout mettre sur le même dénominateur.

⇔ [³/_{(4x + 1)}] – [^{(4x + 1)}/_{(4x + 1)}] > 0
⇔ ^{(3 – (4x + 1))}/_{(4x + 1)} > 0
⇔ ^{(3 – 4x – 1)}/_{(4x + 1)} > 0
⇔ ^{(2 – 4x)}/_{(4x + 1)} > 0

Le membre de gauche est en forme de dénominateur donc on peut appliquer la règle des signes en faisant un tableau de signe.

Je cherche le signe du numérateur avec une mini-inéquation :

On a le signe « + »
quand 2 – 4x ≥ 0
quand -4x ≥ -2
quand ^-4x/_-4 ≤ ^-2/_-4
(on change le sens de l’inégalité car on divise par un nombre négatif de chaque côté)
quand x ≤ ²/₄
quand x ≤ ¹/₂
Cela veut dire que c’est à gauche de ¹/₂ dans le tableau.

On mettra donc le signe « + » à gauche de de ¹/₂.

Pour le signe du dénominateur, on le connait déjà car on l’a fait avant avec le domaine de définition.

Voici donc le tableau de signe du quotient :

Pour conclure sur l’inéquation, comme on veut un membre de gauche strictement supérieur à 0, on sélectionne exclusivement les + du tableau. Soit des x appartenant à

S = ] –¹/₄ ; ¹/₂ [.

On ne sélectionne pas la valeur de x au-dessus de la double-barre (elle ne rentre pas dans le domaine de définition de l’inéquation), ni la valeur de x au-dessus du 0 (inégalité stricte).

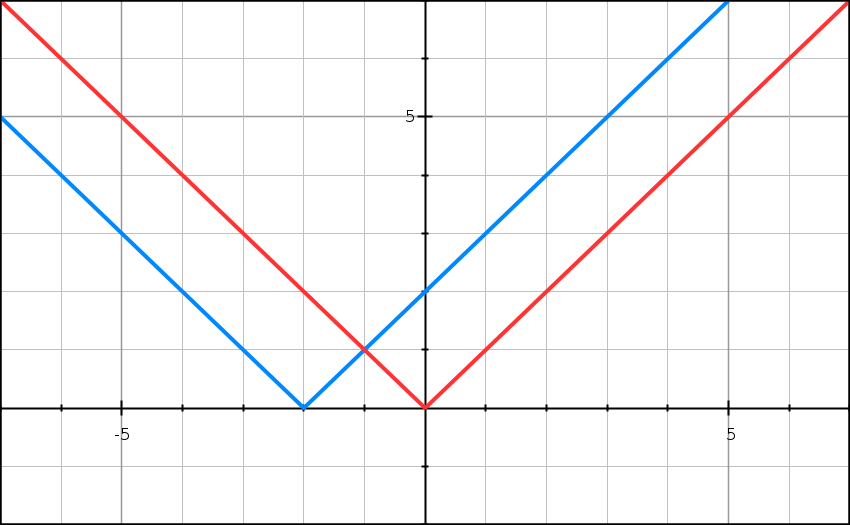
3) (x + 3)² > (2x – 1)² :

Rédaction :

Pour résoudre une inéquation, la première astuce de de tout mettre à gauche en soustrayant le membre de droite.

⇔ (x + 3)² – (2x – 1)² > 0

Carré moins Carré, on retrouve la forme développée de la troisième identité remarquable. On peut la factoriser.

Le A² est (x + 3)²,
donc le A est (x + 3).

Le B² est (2x – 1)²,
donc le B est (2x – 1).

En factorisant, on obtient :

⇔ [(x + 3) + (2x – 1)] × [(x + 3) – (2x – 1)] > 0

⇔ [x + 3 + 2x – 1] × [x + 3 – 2x + 1] > 0
(attention quand on enlève le couple de parenthèses après l’opérateur « moins »)

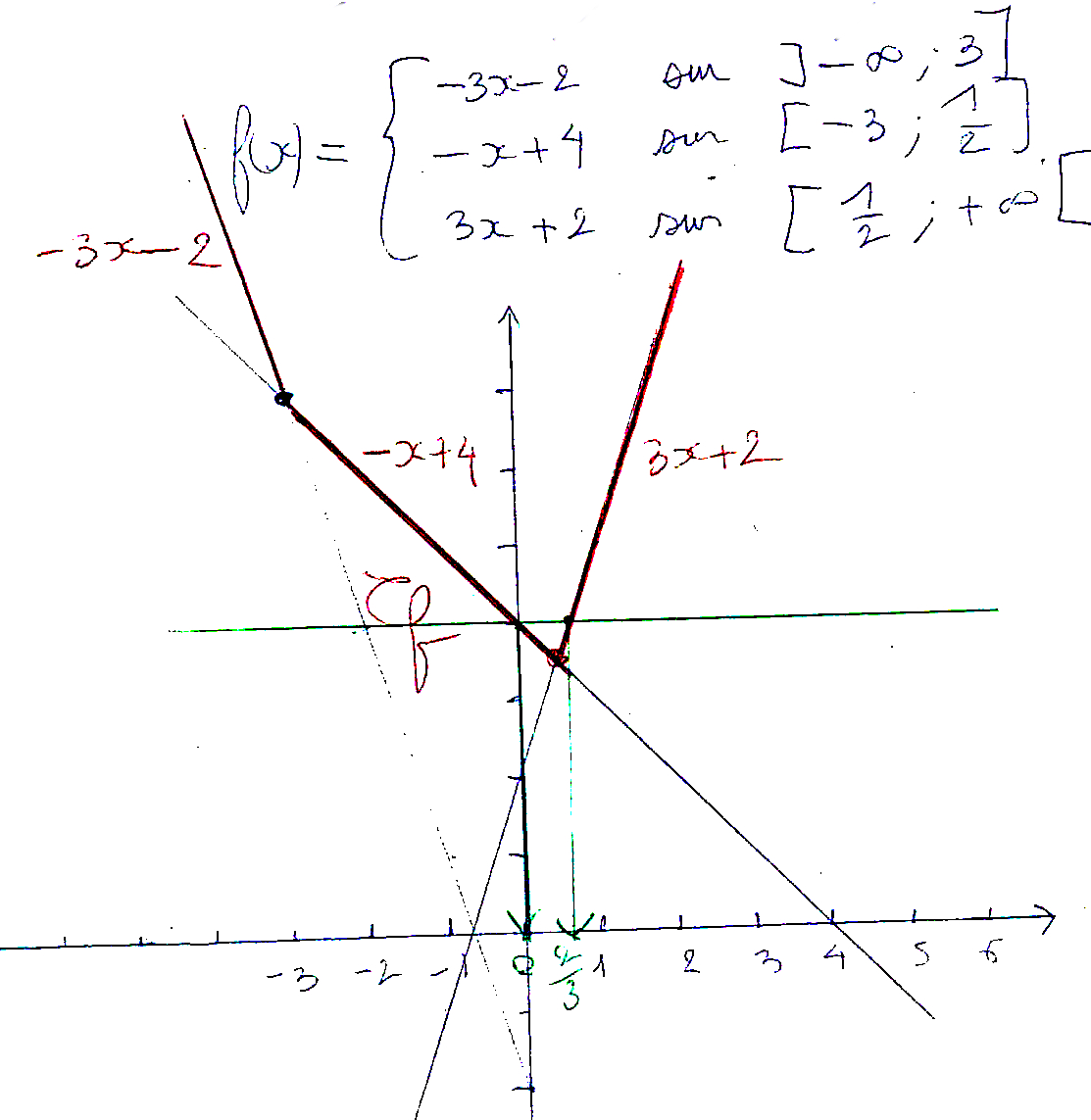
⇔ [3x + 2] × [-x + 4] > 0

⇔ (3x + 2) × (-x + 4) > 0

Pour résoudre une inéquation avec > 0, l’idéal est de construire le tableau de signe de l’expression de gauche et de déterminer les intervalles de x où il y a les « + » (mais pas les « 0 »).

Pour cela, on doit d’abord obtenir les signes de 3x + 2
et de -x + 4 séparément. J’effectue des petites inéquations que j’appelle mini-inéquations.

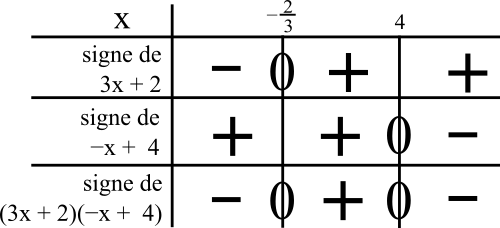
On a le signe « + »
quand 3x + 2 ≥ 0
quand 3x ≥ -2
quand ^2x/₂ ≥ –²/₃
(on garde le sens de l’inégalité car on divise par un nombre positif de chaque côté)
quand x ≥ –²/₃
Cela veut dire que c’est à droite de –²/₃ dans le tableau.

On mettra donc le signe « + » à droite de –²/₃.

On a le signe « + »
quand -x + 4 ≥ 0
quand -x ≥ -4
quand ^-1x/_-1 ≤ ^-4/_-1
(on change le sens de l’inégalité car on divise par un nombre négatif de chaque côté)
quand x ≤ 4
Cela veut dire que c’est à gauche de 4 dans le tableau.

On mettra donc le signe « + » à gauche de 4.

Voici le tableau de signe :

Pour conclure sur l’inéquation, comme on veut un membre de gauche strictement supérieur à 0, on sélectionne exclusivement les + du tableau. Soit des x appartenant à

S = ] –²/₃ ; 4 [.

On ne sélectionne pas les valeur de x au-dessus du 0 (inégalité stricte).

4) 9 – x² + (3 – x)(2x + 6) ≤ 0 :

Rédaction :

Pour résoudre une inéquation avec 0 à droite, il faut faire un tableau de signe de l’expression de gauche.

Mais pour faire un tableau de signe, il nous faut un produit. Et là, on a une soustraction et une addition, il faut factorise.

Avec 9 – x², on a quelque chose de la forme Carré moins Carré, on retrouve la forme développée de la troisième identité remarquable. On peut la factoriser.

Le A² est 9,
donc le A est 3.

Le B² est x²,
donc le B est x.

En factorisant le début, on obtient :

⇔ (3 + x) × (3 – x) + (3 – x)(2x + 6) ≤ 0

La première façon de factoriser est de regarder si on a un facteur commun. Ci-dessous, on voit :

⇔ (3 + x) × (3 – x) + (3 – x)(2x + 6) ≤ 0
⇔ (3 – x) × (3 + x) + (3 – x) × (2x + 6) ≤ 0
On utilise donc la formule de la factorisation avec facteur commun :

Comme c’est un « plus » qu’on a au milieu, on prend la formule avec le « plus », soit :
K × A + K × B

Le K est (3 – x).
Le A est (3 + x).
Le B est (2x + 6).

En forme factorisée, cela donne :
K × (A + B) soit

⇔ (3 – x) × [(3 + x) + (2x + 6)] ≤ 0
⇔ (3 – x) × [3 + x + 2x + 6] ≤ 0
⇔ (3 – x) × [3x + 9] ≤ 0
⇔ (3 – x) × (3x + 9) ≤ 0

Pour résoudre une inéquation avec ≤ 0, l’idéal est de construire le tableau de signe de l’expression de gauche et de déterminer les intervalles de x où il y a les « – » et les « 0 ».

Pour cela, on doit d’abord obtenir les signes de 3 – x
et de 3x + 9 séparément. J’effectue des petites inéquations que j’appelle mini-inéquations.

On a le signe « + »
quand 3 – x ≥ 0
quand -x ≥ -3
quand ^-1x/_-1 ≤ –³/_-1
(on change le sens de l’inégalité car on divise par un nombre négatif de chaque côté)
quand x ≤ 3
Cela veut dire que c’est à gauche de 3 dans le tableau.

On mettra donc le signe « + » à gauche de 3.

On a le signe « + »
quand 3x + 9 ≥ 0
quand 3x ≥ -9
quand ^3x/₃ ≥ ^-9/₃
(on garde le sens de l’inégalité car on divise par un nombre positif de chaque côté)
quand x ≥ -3
Cela veut dire que c’est à droite de -3 dans le tableau.

On mettra donc le signe « + » à droite de -3.

Voici le tableau de signe :

Pour conclure sur l’inéquation, comme on veut un membre de gauche ≤ 0, on sélectionne les « – » et les « 0 » du tableau. Soit des x appartenant à

S = ] -∞ ; -3 ] U [ 3 ; +∞ [.

On sélectionne les valeur de x au-dessus du 0 (inégalité large) donc on met des crochets fermés sur -3 et 3. Toujours des crochets ouverts aux infinis.

¹/_{(5x – 1)} ≤ ¹/_{(x + 2)}
5) Ensemble de définition de l’inéquation :

Rédaction :

Attention, il y a deux fraction avec des x, c’est-à-dire, deux expressions rationnelles. Il faut donc déterminer l’ensemble de définition de l’équation.

Or une expression rationnelle (fraction) est définie si et seulement si son dénominateur est différent de zéro.

On va donc faire les tableau de signe des dénominateur et exclure les valeurs de x qui font que ces dénominateurs sont égaux à zéro.

On a le signe « + »
quand 5x – 1 ≥ 0
quand 5x ≥ 1
quand ^5x/₅ ≥ ¹/₅
(on garde le sens de l’inégalité car on divise par un nombre positif de chaque côté)
quand x ≥ ¹/₅
Cela veut dire que c’est à droite de ¹/₅ dans le tableau.

On mettra donc le signe « + » à droite de ¹/₅.

Ce dénominateur est donc nul quand x = ¹/₅.
Le domaine de définition de l’inéquation sera d’ores et déjà privé de ¹/₅.

On a le signe « + »
quand x + 2 ≥ 0
quand x ≥ -2
Cela veut dire que c’est à droite de -2 dans le tableau.

On mettra donc le signe « + » à droite de -2.

Ce dénominateur est donc nul quand x = -2.
Le domaine de définition de l’inéquation sera d’ores et déjà privé de -2.

En rassemblant les deux valeurs exclues ¹/₅ et -2, on peut affirmer que le domaine de définition est l’ensemble des réels privé de ces deux valeur.
D = R privé de {-2 ; ¹/₅}
D = ] -∞ ; -2 [ U ] -2 ; ¹/₅ [ U ] ¹/₅ ; +∞ [

^{(-4x + 3)}/_{[ (5x – 1)(x + 2) ]} ≤ 0
6) Équivalence de l’inéquation 5) à celle ci-dessus :

Rédaction :

Pour résoudre une inéquation, la première astuce de de tout mettre à gauche en soustrayant le membre de droite.

¹/_{(5x – 1)} ≤ ¹/_{(x + 2)}
⇔ ¹/_{(5x – 1)} – ¹/_{(x + 2)} ≤ 0

Pour résoudre cette inéquation avec une fraction et une soustraction, l’astuce est de tout mettre sur le même dénominateur.
On multiplie donc ici, les dénominateurs entre eux pour obtenir le dénominateur commun.

Pour faire bien, on multiplie le premier numérateur par le second dénominateur et le second numérateur par le premier dénominateur. Comme ci-dessous :

⇔ ¹/_{(5x – 1)} × ^{(x + 2)}/_{(x + 2)} – ¹/_{(x + 2)} × ^{(5x – 1)}/_{(5x – 1)} ≤ 0

⇔ ^{(1(x + 2))}/_{[ (5x – 1)(x + 2) ]} – ^{(1(5x – 1))}/_{[ (5x – 1)(x + 2) ]} ≤ 0

Les dénominateurs sont les mêmes, on peut rassembler les numérateurs sur la même barre de fraction.

⇔ ^{[ 1(x + 2) – 1(5x – 1) ]}/_{[ (5x – 1)(x + 2) ]} ≤ 0
⇔ ^{[ (x + 2) – (5x – 1) ]}/_{[ (5x – 1)(x + 2) ]} ≤ 0
⇔ ^{[ x + 2 – 5x + 1 ]}/_{[ (5x – 1)(x + 2) ]} ≤ 0
⇔ ^{[ -4x + 3 ]}/_{[ (5x – 1)(x + 2) ]} ≤ 0
⇔ ^{(-4x + 3)}/_{[ (5x – 1)(x + 2) ]} ≤ 0

7) Résolution de l’équation 5) :

Rédaction :

Cela revient à résoudre la dernière inégalité.
⇔ ^{(-4x + 3)}/_{[ (5x – 1)(x + 2) ]} ≤ 0

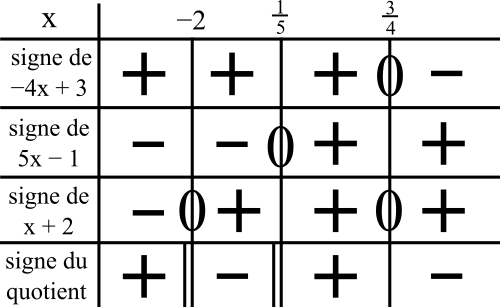
Pour résoudre une inéquation avec ≤ 0, l’idéal est de construire le tableau de signe de l’expression de gauche et de déterminer les intervalles de x où il y a les « – » et « 0 ».

Évidemment, il faut un produit de facteurs ou des quotients pour pouvoir appliquer la règle des signes et faire ce tableau de signe. C’est le cas avec (-4x + 3), (5x – 1) et (x + 2). Il y a une barre de fraction (soit diviser) et un produit en bas (soit multiplier).

On peut donc refaire les mini-inéquations.

On a le signe « + »
quand -4x + 3 ≥ 0
quand -4x ≥ -3
quand ^-4x/_-4 ≤ ^-3/_-4
(on change le sens de l’inégalité car on divise par un nombre négatif de chaque côté)
quand x ≤ ³/₄
Cela veut dire que c’est à gauche de ³/₄ dans le tableau.

On mettra donc le signe « + » à gauche de ³/₄.

On a le signe « + »
quand 5x – 1 ≥ 0
quand 5x ≥ 1
quand ^5x/₅ ≥ ¹/₅
(on garde le sens de l’inégalité car on divise par un nombre positif de chaque côté)
quand x ≥ ¹/₅
Cela veut dire que c’est à droite de ¹/₅ dans le tableau.

On mettra donc le signe « + » à droite de ¹/₅.

On a le signe « + »
quand x + 2 ≥ 0
quand x ≥ -2
Cela veut dire que c’est à droite de -2 dans le tableau.

On mettra donc le signe « + » à droite de -2.

Ce qui donne le tableau de signe suivant :

Pour conclure sur l’inéquation, comme on veut un membre de gauche ≤ 0, on sélectionne les « – » et les « 0 » du tableau. Soit des x appartenant à

S = ] -2; ; ¹/₅ [ U [ ³/₄ ; +∞ [.

On sélectionne les valeurs de x au-dessus du 0 (inégalité large) donc on met des crochets fermés sur ³/₄. Toujours des crochets ouverts aux infinis et on les mets aussi aux valeurs exclues -2 et ¹/₅ (là où il y a les doubles-barres).

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) a est l’abscisse du point, sa « largeur ».
Donc je prends 1 sur l’axe des abscisses.

f(a) est l’image, soit l’ordonnée du point, sa « hauteur ».
La courbe est en bas, donc je descends verticalement vers la courbe et je note l’ordonnée du point : c’est -4.
Donc f(1) = -4.

f ‘ (a) est la pente de la tangente de la courbe. On détermine la droite-tangente que l’on pose sur la courbe et on regarde le coefficient directeur.

Je prends le même point d’abscisse et je vois que la tangente est horizontale car on a un replat (un minimum ici) de la courbe. Donc le coefficient directeur vaut 0 car la tangente à Cf est parallèle à l’axe des abscisses (horizontale).
Donc f ‘ (1) = 0.

2) Quand la pente est positive, c’est-à-dire quand f ‘ (x) > 0, f est strictement croissante (et vice-versa).

Quand la pente est négative, c’est-à-dire quand f ‘ (x) < 0, f est strictement croissante (et vice-versa).

Quand f ‘ (x) = 0, on a un replat de Cf.

Grâce au graphique, on peut faire le tableau de variation de f, puis en déduire le signe de f ‘ (x).

Comme f ‘ (x) est négative et devient positive après l’abscisse x = 1, seule la courbe C₁ convient.

3) On a f(x) = ^{(x2 – 6x – 7)}/_{(x + 2)}.

Donc f(x) = ^u(x)/_v(x)
avec
u(x) = x² – 6x – 7,
u ‘ (x) = 2x – 6 – 0,
v(x) = x + 2,
v ‘ (x) = 1 + 0.

La formule de la dérivée d’un quotient est :

Donc Numérateur = (2x – 6) × (x + 2) – [ (x² – 6x – 7) × 1 ]
= 2x² + 4x – 6x – 12 – x² + 6x + 7
= x² + 4x – 5

Donc f ‘ (x) = ^{(x2 + 4x – 5)}/_{(x + 2)²}

4) Pour étudier les variations de f, on détermine le signe de f ‘ (x) dans un tableau de signe. Je mets ici une ligne pour le numérateur et une ligne pour le dénominateur.

Pour le signe de x² + 4x – 5, comme c’est un polynôme du second degré, on calcule le discriminant.

Δ = b² – 4ac
= 4² – 4 × 1 × (-5)
= 16 + 20 = 36 > 0 soit deux racines :

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-4 – √36)}/_{(2 × 1)}
= ^{(-4 – 6)}/₂
= ^-10/₂
= -5

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-4 + √36)}/_{(2 × 1)}
= ^{(-4 + 6)}/₂
= ²/₂
= 1

Un polynôme du second degré est du signe de a à l’extérieur des racines quand Δ > 0 car la parabole coupe deux fois l’axe des abscisses.
Comme a = 1 > 0, la parabole « sourit » et le polynôme du second degré est positif avant -5 et après 1. Il est négatif entre -5 et 1. Puis nul entre -5 et 1.

Pour le (x + 2)², un carré est toujours positif ou nul. Ici, il est nul en -2. Comme la fonction n’est pas définie en -2, il sera ici toujours strictement positif : on met un + dans la ligne.

Cela donne le tableau suivant :

J’ai exclu l’abscisse -2 des lignes des tableaux de signe et variation. Il y a donc une double-barre à gauche.

Petit rappel pour la variation de f :

Quand la pente est positive, c’est-à-dire quand f ‘ (x) > 0, f est strictement croissante.
Quand la pente est négative, c’est-à-dire quand f ‘ (x) < 0, f est strictement decroissante.

Bonne compréhension,
Sylvain Jeuland