Exercice de maths sur les dérivées. Fonctions, dérivation, pentes, première, coordonnées, tangente, courbe, polynôme et systèmes.
Exercice N°051 :
Une entreprise souhaite fabriquer pour de jeunes enfants des toboggans dont le profil a l’allure de la courbe ci-dessous. L’objet de l’exercice est de modéliser ce profil à l’aide de la courbe représentative C d’une fonction définie sur l’intervalle [0 ; 3] vérifiant les conditions suivantes :
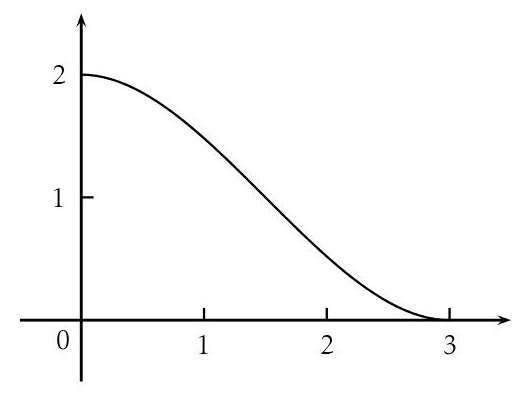
(*) La courbe C passe par les points A(0 ; 2) et B(3 ; 0).
(*) La courbe C admet en chacun des points A et B une tangente parallèle à l’axe des abscisses.
Le bureau d’étude pense que l’on peut modéliser le profil du toboggan à l’aide d’une fonction polynôme de degré 3 :
f(x) = ax3 + bx2 + cx + d
avec a, b, c et d étant quatre nombres réels.
1) Démontrer que les valeurs f(0) et f ‘ (0) permettent d’obtenir
c = 0 et d = 2.
2) Trouver alors a et b grâce aux valeurs de f(3) et f ‘ (3).
3) Déterminer les coordonnées du point de la courbe de f d’abscisse 1.
4) Déterminer le coefficient directeur de la tangente en ce point d’abscisse 1.
Bon courage,
Sylvain Jeuland
Pour avoir la suite du corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : Fonctions, dérivation, pentes, première.
Exercice précédent : Dérivation – Fonctions, méthodes et calculs classiques – Première

