Maths de première : exercice d’exponentielle avec équations et variation. Fonction, inéquations, calculs de dérivées, tableau de signe.
Exercice N°660 :
Exercice N°660 :
1-6) Résoudre les équations suivantes :
1) ex = -4 Lis la suite »
Maths de première : exercice de dérivation avec optimisation de volume. Calcul, surface, tableaux de signe et de variation, maximum.
Exercice N°043 :
Exercice N°043 :
Un vendeur de berlingots veut faire fabriquer une nouvelle boîte de présentation pour Noël. Elle aura la forme d’un prisme droit dont deux des faces sont deux rectangles de 20 cm de longueur sur 5 cm de largeur.
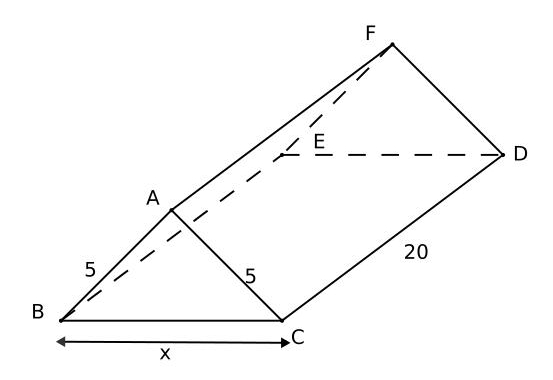
Une section de ce prisme par un plan perpendiculaire à la face BCDE est le triangle ABC isocèle en A. La longueur BC = x représente l’écartement entre les deux rectangles.
Le but du problème est de déterminer x tel que le volume de cette boîte soit le plus grand possible.
1) Quelles sont les valeurs possibles pour x ? Lis la suite »
Maths de seconde sur les fonctions affines. Exercice de droite, point d’intersection, sécantes, système d’équation, fraction, inconnues.
Exercice N°622 :
Exercice N°622 :
Soit (d1) la droite d’équation
y = -2 x + 1,
et (d21) la droite d’équation
y = (1/2)x + 1.
1) Faire une figure (tracer les deux droites et placer les points). Lis la suite »
Exercice de maths de seconde sur système d’équation et second degré. Coefficient de polynôme, points, courbe, calculs de variables.
Exercice N°620 :
Exercice N°620 :
On considère la fonction f définie par
f(x) = x2 + ax + b
où a et b sont des nombres réels que l’on cherche à déterminer. On souhaite que la courbe représentative Cf de cette fonction f, passe par
les points A(−1 ; 6) et B(1 ; 2).
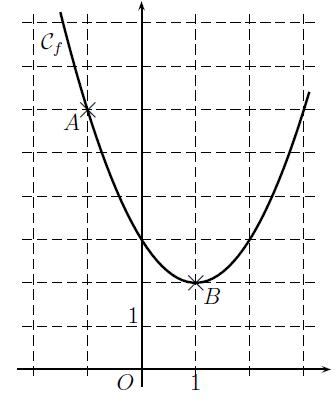
1) Déterminer les réels a et b et donner l’expression de la fonction f vérifiant ces deux conditions. Lis la suite »
Maths de première : exercice sur sens de variation de suite. Croissance et décroissance. Fonction polynôme, formes récurrente, explicite.
Exercice N°110 :
Exercice N°110 :
1) Déterminer le sens de variation de la suite (un) définie par la forme explicite :
un = 2n2 − 1. Lis la suite »
Maths de première : exercice sur fonction trigonométrique cosinus avec paire, impaire, périodicité, tableau de valeurs, courbe à tracer.
Exercice N°728 :
Exercice N°728 :
Soit f la fonction définie sur R par
f(x) = 5cos (2x + π/3).
On note Cf la représentation graphique de f dans le plan graphique
(O ; →i ; →j).
1) La fonction f est-elle paire ? Impaire ? Lis la suite »
Exponentielle – Équation, continuité, suite, récurrence – Terminale
13 novembre 2021
Exercice de maths sur la fonction exponentielle, suite, récurrence, terminale, continuité, équations, convergence, raisonnement, variations.
Exercice N°284 :
Exercice N°284 :
Le but de l’exercice est de démontrer que l’équation (E) ∶
xex = 1
admet une unique solution dans l’ensemble R des nombres réels, et de construire une suite qui converge vers cette unique solution.
Existence et unicité de la solution :
On note f la fonction définie sur R par
f(x) = x − e−x.
1) Démontrer que x est solution de l’équation (E)
si et seulement si f(x) = 0. Lis la suite »
Maths de terminale: Exercice de suite avec variation de fonction, récurrence, inégalités, termes, bornes, convergence, limite.
Exercice N°190 :
Exercice N°190 :
On modélise le nombre un de foyers français possédant un téléviseur à écran plat (en millions) en fonction de l’année (2005 + n) par la suite u définie par,
u0 = 1
et pour tout entier naturel n :
un+1 = (1/10)un(20 − un).
Soit la fonction f définie sur [0 ; 20] par :
f(x) = (1/10)x(20 − x).
1) Étudier les variations de f sur [0 ; 20]. Lis la suite »
Maths de première : exercice de dérivation avec équation de tangente. Fonction rationnelle, variation, courbe, graphique, tracer la droite.
Exercice N°293 :
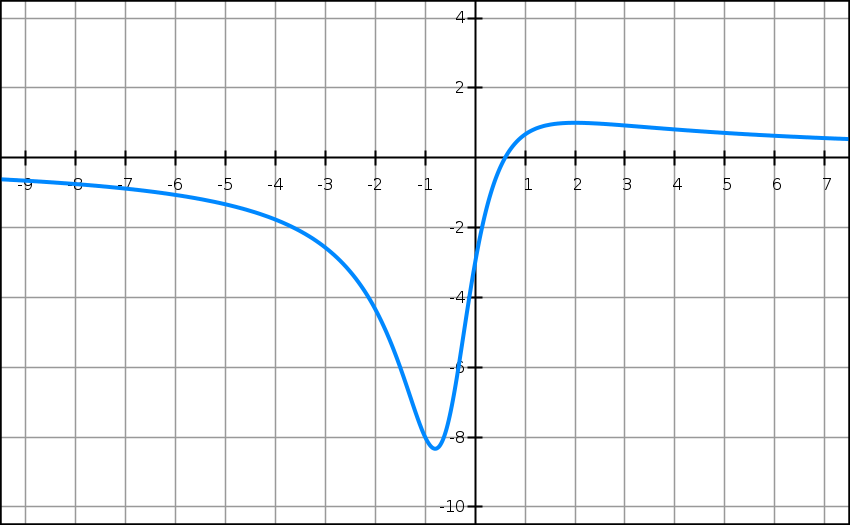
Soit f la fonction définie sur R par
f(x) = (5x − 3)/(x2 + x + 1).
On note Cf sa courbe représentative dans le plan muni d’un repère.
1) On note f ‘ la dérivée de la fonction f. Calculer f ‘ (x). Lis la suite »
Maths de première : exercice sur fonction rationnelle, dérivée, courbe représentative, repère, variations, équation de la tangente.
Exercice N°291 :
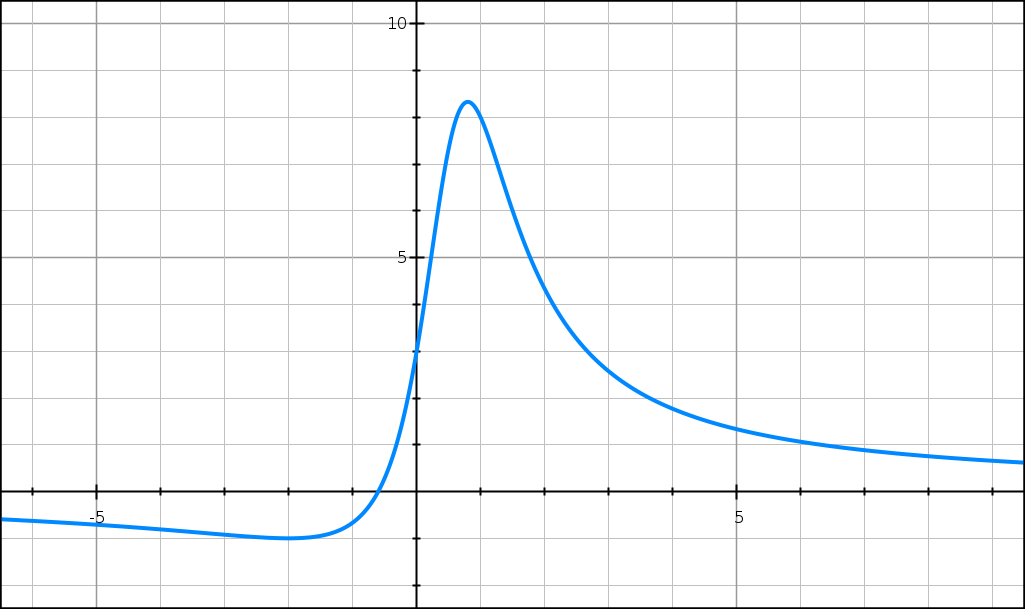
Soit f la fonction définie sur R par l’expression suivante :
f(x) = (5x + 3)/(x² − x + 1).
On note Cf sa courbe représentative dans le plan muni d’un repère orthonormé.
1) Montrer que la dérivée de la fonction f est la fonction f ‘ définie sur R par l’expression :
f ‘ (x) = (− 5x² −6x + 8)/(x²− x + 1)². Lis la suite »
