frenchmaths.com (par Sylvain Jeuland)

Maths de première : exercice de dérivation avec équation de tangente. Fonction rationnelle, variation, courbe, graphique, tracer la droite.

Exercice N°293 :

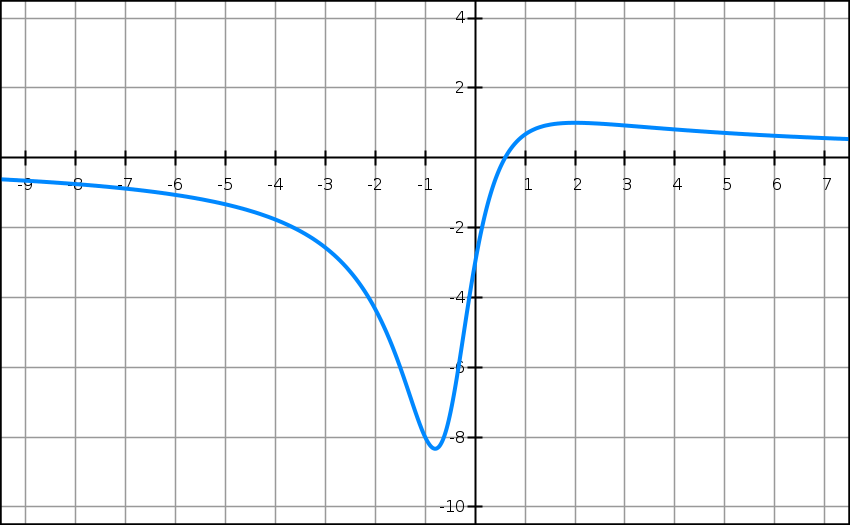
Soit f la fonction définie sur R par
f(x) = ^{(5x − 3)}/_{(x² + x + 1)}.
On note C_f sa courbe représentative dans le plan muni d’un repère.

1) On note f ‘ la dérivée de la fonction f. Calculer f ‘ (x).

2) Étudier les variations de la fonction f.

3) Donner une équation de la tangente T_A à la courbe C_f
au point A d’abscisse −³/₂.

4) Représenter la tangente T_A sur le graphique ci-dessus.

Partie indépendante :

Soit g la fonction définie sur R par
g(x) = x³ – 3x².
On note C_g sa courbe représentative dans le plan muni d’un repère.

5) Dresser le tableau de variation complet de la fonction g avec les extremums locaux inclus.

6) Déterminer un encadrement précis de g sur [-2 ; 2] puis sur [0 ; 4].

On considère le point B de C_g d’abscisse b.
7) Exprimer en fonction de b l’équation de la tangente à C_g en B (sous forme développée et réduite). On note T_B cette tangente.

8) Soit M le point de coordonnées (2 ; 0). Déterminer la ou les valeurs de b pour lesquelles la tangente T_B passe par M.

Bon courage,
Sylvain Jeuland

Mots-clés de l’exercice : exercice, dérivation, équation, tangente.

Exercice précédent : Dérivation – Variations, coefficients, rationnelle – Première