Maths de première : exercice de dérivation avec fonction rationnelle. Tableau de variation, définition du nombre dérivé, calcul, coefficient.
Exercice N°292 :

Exercice N°292 :
Soit f une fonction définie et dérivable sur l’intervalle ]−1/2 ; +∞[ dont le tableau des variations est donné ci-dessous.
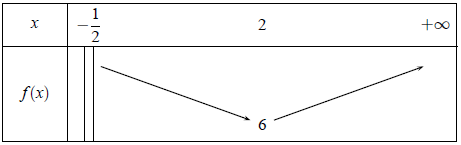
1) On note f ‘ la dérivée de la fonction f. Déterminer f ‘ (2).
2) Déterminer les réels a et b tels que
f(x) = ax + b + [ 25/(2x + 1) ].
On admet que f est la fonction définie sur l’intervalle ]−1/2 ; +∞[
par f(x) = 2x − 3 + [ 25/(2x + 1) ].
3) Justifier par le calcul les résultats obtenus dans le tableau de variation.
Bon courage,
Sylvain Jeuland
Exercice précédent : Dérivation – Fonction rationnelle, variation, tangente – Première

