frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Simplifier ^→u = ^→HF + ^→SU + ^→RS + ^→UH :

Quand tu as une expression vectorielle, regarde si tu peux aligner les mêmes lettres les unes après les autres. Si un vecteur se termine par C (par exemple), essaie de voir si tu peux en trouver un autre qui commence par C. Regroupe les comme ci-dessous :

Cela veut dire que si tu pars d’un point A vers un point C, et que tu repars de ce même point C vers le point B ;;; c’est comme si tu partais du point A directement vers le point B. C’est le même déplacement car même départ et même arrivée.

Du coup, avec ^→u, mets les vecteurs en ordre en rapprochant les mêmes points.

Rédaction :

^→u = ^→HF + ^→SU + ^→RS + ^→UH
= ^→RS + ^→SU + ^→UH + ^→HF
= ^→RU + ^→UH + ^→HF
= ^→RH + ^→HF
= ^→;RF
Toutes les simplifications sont dues à la relation de Chasles.

2) Simplifier ^→v = ^→OC – ^→OB + ^→AB :

Il y a un « moins- » devant ^->OB ? Il faut un « plus+ » pour refaire une éventuelle relation de Chasles. Pour cela, échange les lettres pour faire
–^→OB = +^→BO

Rédaction :
^→v = ^→OC – ^→OB + ^→AB
= ^→OC + ^→BO + ^→AB
= ^→AB + ^→BO + ^→OC
= ^→AO + ^→OC
= ^→AC
Toutes les simplifications sont dues à la relation de Chasles.

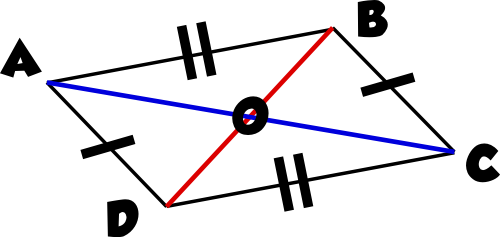
3) Avec ABCD parallélogramme de centre O, démontrer que 2^→AB + 2^→AD – ^→AC = 2^→AO :

Il faut un dessin du parallélogramme ABCD.

Comme on veut arriver à du ^→AO, il faut transformer
le ^→AC en 2^→AO car c’est une égalité du parallélogramme comme tu peux le voir sur le dessin.

De plus, la formule principale du parallélogramme donne :

On peut donc remplacer ^→AB par ^→DC dans l’expression pour ne plus avoir le B.

Rédaction :

On part du membre de gauche pour arriver au droit.
2^→AB + 2^→AD – ^→AC
= 2^→DC + 2^→AD – ^→AC (car ABCD est un parallélogramme)
= 2^→DC + 2^→AD – 2^→AO (car O est le milieu de [AC])
= 2^→AD + 2^→DC – 2^→AO
= 2(^→AD + ^→DC) – 2^→AO
= 2^→AC – 2^→AO
= 2×2^→AO – 2^→AO (car O est le milieu de [AC])
= 2^→AO.
On arrive au membre de droit. Donc on a bien :
2^→AB + 2^→AD – ^→AC = 2^→AO.

4) Avec 3^→MA + ^→MB = ^→0,
exprimer ^→AM en fonction de ^→AB :

Ici, on veut obtenir ^→AM et ^→AB à partir des vecteurs ^→MA et ^→MB.
^→AM et ^→MA sont opposés.
Mais dans ^→MB, il n’y a ni ^→AM, ni ^→AB. Il manque le point A.
Quand il manque un point, il faut l’insérer avec la relation de Chasles.
Ici ^→MB = ^→MA + ^→AB.

Rédaction :

3^→MA + ^→MB = ^→0
⇔ -3^→AM + ^→MB = ^→0
⇔ -3^→AM + ^→MA + ^→AB = ^→0
⇔ -3^→AM – ^→AM + ^→AB = ^→0
⇔ -4^→AM + ^→AB = ^→0
⇔ -4^→AM = –^→AB
⇔ ^→AM = ¹/₄^→AB (en divisant par -4).

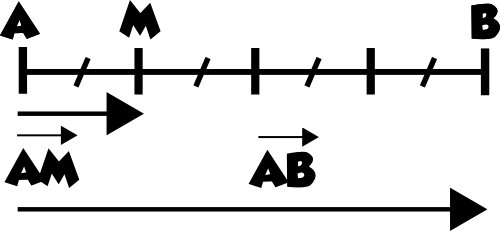
5) Placer le point M sur une figure :

Rédaction :

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Développer une expression, c’est transformer un produit (avec une multiplication comme opération centrale) en somme. Par exemple, x(3x + 6) vaut x « fois » (3x + 6). C’est un produit. Avec la distributivité, on peut transformer cette expression en somme.
k×(a + b) = k×a + k×b
Cela donne : x×3x + x×6.

2) Factoriser une expression, c’est transformer une somme (avec une addition ou soustraction comme opération centrale) en produit. Par exemple, 8x² – 5x est une somme avec « moins » (c’est-à-dire une différence ou soustraction). Avec la distributivité dans l’autre sens,
k×a + k×b = k×(a + b),
cela donne x×(8x – 5).

3) A(x) = (2x + 3)(5 – x) – (x + 3)(3x – 1)
On utilise la double-distributivité
(a + b)(c + d) = a×c + a×d + b×c + b×d.
= 2x×5 + 2x×(-x) + 3×5 + 3×(-x) – [ x×3x + x×(-1) + 3×3x + 3×(-1) ]
(Attention à bien mettre des crochets quand on développe après un moins)
= 10x – 2x² + 15 – 3x – [ 3x² – x + 9x – 3 ]
= 10x – 2x² + 15 – 3x – 3x² + x – 9x + 3
= -5x² – x + 18.

4) B(x) = (x – 1)(x – 2)(x – 3) :
Ici on a trois facteurs à développer. Développons deux à deux en mettant un crochet autour des deux premières parenthèses.
= [(x – 1)(x – 2)](x – 3)
= [x² – 2x – x + 2](x – 3)
= [x² – 3x + 2](x – 3)
= x²×x + x²×(-3) + (-3x)×x + (-3x)×(-3) + 2x + 2×(-3)
= x³ – 3x² – 3x² + 9x + 2x – 6
= x³ – 6x² + 11x – 6.

5) M(x) = (4x – 7)(2x – 1) – (7x + 1)(1 – 2x) :
Ici, on reconnait presque un facteur commun à ceci prêt qu’il y a deux signes opposés : (2x – 1) et (1 – 2x).
On doit donc multiplier l’un des deux par (-1) : (1 – 2x) = (-1)(2x – 1)
On obtient donc :
M(x) = (4x – 7)(2x – 1) – (7x + 1)(-1)(2x – 1)
= (4x – 7)(2x – 1) – (-1)(7x + 1)(2x – 1)
= (2x – 1)[(4x – 7) –(-1)(7x + 1)]
= (2x – 1)[4x – 7 + 7x + 1]
= (2x – 1)[11x – 6]

6) N(x) = (5x – 1)(3x + 2) – 4 + 9x² :

Ici, il est difficile de savoir quoi faire. Il faut s’y connaître un peu.
Je reconnais des carrés à droite. On a 4 = 2² et 9x² = (3x)².
On pourrait avoir du a² – b² en forme développée mais il y a un plus entre les deux termes et un moins avant. Je propose donc de mettre d’abord le 9x² puis ensuite le -4 pour bien obtenir a² – b².

Donc N(x) = (5x – 1)(3x + 2) + 9x² – 4.
Maintenant, d’après a² – b², on obtient (a + b)(a – b).
= (5x – 1)(3x + 2) + (3x – 2)(3x + 2)
On voit le facteur commun (3x + 2). On peut factoriser avec k×(a + b).
= (3x + 2)×[ (5x – 1) + (3x – 2) ]
= (3x + 2)×[5x – 1 + 3x – 2]
= (3x + 2)×[8x – 3].

7) Q(x) = (x – 1)(2x – 3) + 3(4x + 1)(x – 1) :
Le facteur commun est (x – 1) donc on peut factoriser
de k×a + k×b vers k×(a + b).
= (x – 1)[ (2x – 3) + 3(4x + 1) ]
= (x – 1)[ 2x – 3 + 3×4x + 3×1 ]
= (x – 1)[ 14x ]
= 14x(x – 1).

8) (a + b)³
= (a + b)²(a + b)
= [ (a + b)² ](a + b)
= [ a² + 2ab + b² ](a + b)
= a³ + a²b + 2a²b + 2ab² + b²a + b³
= a³ + 3a²b + 3ab² + b³.

9) (a – b)³
= (a – b)²(a – b)
= [ (a – b)² ](a – b)
= [ a² – 2ab + b² ](a – b)
= a³ – a²b – 2a²b + 2ab² + b²a – b³
= a³ – 3a²b + 3b²a – b³.

Bonne compréhension,
Sylvain Jeuland