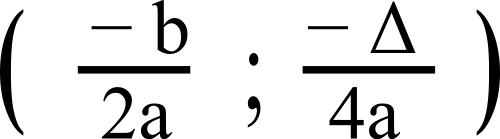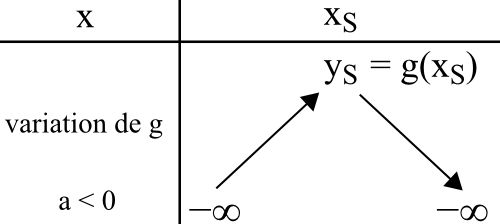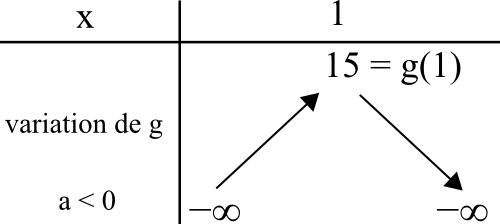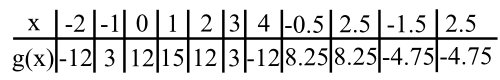frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Rédaction :

Le sommet d’une parabole est donné par les coordonnées α et β du cours de maths. Je préfère les appeler x_S et y_S. Les formules sont :

Ici a = -3, b = 6, c = 12.

x_S = ^-b/_2a = ^-6/_(2(-3))
= ^-6/_-6 = 1

Δ = b² – 4ac
= 6² – 4 × (-3) × 12
= 36 + 4 × 3 × 12
= 36 + 144
= 180

y_{S = ^-Δ/4a = ^-180/(4(-3))
= ^-12/-6 = 15}

On peut calculer aussi l’ordonnée du sommet y_S en prenant l’image f(x_S). On peut aussi utiliser α et β pour nommer l’abscisse et l’ordonnée du sommet.

Donc les coordonnées du sommet S sont (1 ; 15).

2) Rédaction :

Comme on a les coordonnées du sommet, on sait où s’arrêtent les flèches.
Regardons le signe de « a ». C’est -3 donc il est négatif.

(Hors-rédaction : l’atmosphère/ambiance est négative, la parabole ne sourit pas.)

Du coup, la parabole monte puis descend. De même pour les flèches. J’obtiens le tableau de variation suivant.

Pour dessiner une courbe, il faut faire un tableau de valeurs. Par exemple de 1 en 1 en partant de (-3).

(Tu peux le faire à la calculatrice à l’aide de la fonction table. Ou alors tu dessines le tableau sur la copie en calculant un par un en mettant bien des parenthèses autour des nombres négatifs. Quand c’est espacé en hauteur, tu peux calculer de demi en demi : 0.5, 1.5, etc)

3) Rédaction :

3x² – 4x – 4 > -3x² + 6x + 12
⇔ 3x² – 4x – 4 – (-3x² + 6x + 12) > 0
⇔ 3x² – 4x – 4 + 3x² – 6x – 12 > 0
⇔ 6x² – 10x – 16 > 0

Pour résoudre une inéquation plus grand ou plus petit que 0, je dois faire un tableau de signe.

Comme c’est du second degré, je calcule le discrimant
Δ = b² – 4ac
= (-10)² – 4 × 6 × (-16)
= 100 + 384 = 484 > 0

Donc on a deux racines x₁ et x₂ :

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-(-10) – √484)}/_{(2 × 6)}
= ^{(10 – 22)}/₍₁₂₎
= ^-12/₁₂
= -1

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-(-10) + √484)}/_{(2 × 6)}
= ^{(10 + 22)}/₍₁₂₎
= ³²/₁₂
= ⁸/₃

Le tableau de signe est de la forme (on rappelle que a > 0) :

Donc on prend seulement les « plus+ » et pas les zéros car l’inégalité est stricte.

S = ]-∞ ; -1[ U ]⁸/₃ ; +∞[

4) Rédaction :

3x² – 4x – 4 > -3x² + 6x + 12
C’est quand f(x) > g(x) d’après les données.
C’est quand la courbe C_f est strictement au dessus de la courbe C_g.

Si on entoure les portions de courbe qui conviennent et qu’on redescend verticalement sur l’axe des abscisses, on retrouve la réunion d’intervalle précédente.

5) Rédaction :

A_g est égale à la moitié de l’aire du carré ABCD
⇔ A_g = 0.5 × A_ABCD
⇔ AM² + (AB-AM)² = 0.5 × AB²

On pose x = AM (ça marche toujours comme ça dans ce style d’exercice).

⇔ x² + (8 – x)² = 0.5 × 8²
⇔ x² – 8² + 2 × 8 × x + x² = 0.5 × 64
⇔ x² + 64 – 16x + x² = 32
⇔ 2x² – 16x + 64 – 32 = 0
⇔ 2x² – 16x + 32 = 0

Comme tous les coefficients sont paire, je simplifie cette équation par 2 pour simplifier.

⇔ x² – 8x + 16 = 0

Je peux résoudre avec le discriminant Δ mais je préfère ici utiliser une identité remarquable.

⇔ x² – 2 × 4 × x + 16 = 0
⇔ (x – 4)² = 0
⇔ x – 4 = 0 (Un carré est nul si et seulement si son contenu est nul).
⇔ x = 4

Donc AM = 4 et il existe une seule position de M qui convient à cette égalité d’aires. C’est le milieu de [AB].

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Sur l’écran de votre calculatrice, tracer (P) et (D) et conjecturer le nombre de points d’intersection de (P) et (D).

Rédaction :

Ce n’est pas très précis. Je conjecture qu’il y a un point d’intersection entre (P) et (D).

2) Déterminer par le calcul les abscisses des points d’intersection de (P) et (D).

Rédaction :

Je donne des noms aux deux fonctions associées à (P) et (D).

p(x) = -9x² + 60x – 80
d(x) = 5x + 4

Pour trouver les points d’intersection des deux courbes, il faut qu’elles sont la même hauteur (image) pour le le même « x ».
Je résous :

(P) et (D) se coupent quand
p(x) = d(x)
⇔ -9x² + 60x – 80 = 5x + 4
⇔ -9x² + 60x – 80 – (5x + 4) = 0
⇔ -9x² + 60x – 80 – 5x – 4 = 0
⇔ -9x² + 55x – 84 = 0

Δ = b² – 4ac
= 55² – 4 × (-9) × (-84)
= 3025 – 3024
= 1 > 0

Donc il y a deux solutions distinctes.

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-55 – √1)}/_{(2 × (-9))}
= ^(-56)/_((-18))
= ²⁸/₉

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-55 + √1)}/_{(2 × (-9))}
= ^(-54)/_((-18))
= 3

Du coup, (P) et (D) ony deux points d’intersection, en x = 3 et x = ²⁸/₉.

3) Déterminer la forme canonique de f :

Rédaction :

On a f(x) = 2x² + 2x – 24.
La forme canonique d’une fonction du second degré est :

x^S = α = abscisse du sommet
y^S = β = ordonnée du sommet

Ces coordonnées (x^S ; y^S) sont données par :

Ici a = 2, b = 2, c = -24.

x_S = ^-b/_2a = ^-2/_(2×2)
= ^-2/₄
= ^-1/₂

Δ = b² – 4ac
= 2² – 4 × 2 × (-24)
= 4 + 4 × 2 × 24
= 4 + 192
= 196

y_{S = ^-Δ/4a = ^-196/(4×2)
= ^-196/8
= ^-49/2}

Donc les coordonnées du sommet S sont (2 ; –⁴⁹/₂).

On peut aussi calculer y_S avec
f(x_S) = f(^-1/₂) = 2 × ^(-1/₂₎² + 2 × ^(-1/₂₎ – 24
= 2 × ¹/₄ – 1 – 24
= ¹/₂ – ²/₂ – ⁴⁸/₂
= –⁴⁹/₂

4) Factoriser f(x) :

Rédaction :

Comme Δ est positif, il y a deux racines x1 et x2 (quand c’est nul, x1 = x2).
La forme factorisée d’un polynôme du second degré est :

Ici a = 2, b = 2, c = -24, Δ = 196

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-2 – √196)}/_{(2 × 2)}
= ^{(-2 – 14)}/₍₄₎
= ^-16/₄
= -4

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-2 + √196)}/_{(2 × 2)}
= ^{(-2 + 14)}/₍₄₎
= ¹²/₄
= 3

Donc la forme factorisée est f(x) = 2 × (x – (-4)) × (x – 3).

5) Coordonnées des points d’intersection de (C) avec l’axe des abscisses et avec l’axe des ordonnées :

Rédaction :

Les points d’intersections de (C) avec l’axe des abscisses, c’est quand f(x) = 0.
J’ai déjà résolu cette équation en 4).
C’est pour x = -4 et x = 3. Et leur ordonnée y vaut 0.
Donc ces points sont (0 ; -4) et (0 ; 3).

Si (C) coupe l’axe des ordonnées (ce qui donnera ce point d’intersection), c’est que l’abscisse x est égal à 0 car l’axe des ordonnées a pour équation x = 0.
Pour le calcul de l’ordonnée, je rassemble y = f(x) et x = 0, cela fait y = f(0).
y = f(0) = 2 × 0² +2 × 0 – 24
= -24.
Le point d’intersection a pour coordonnées (0 ; -24).

6) Position de (C) par rapport à l’axe des abscisses :

(C) est au dessus de l’axe des abscisse quand f(x) > 0 et est en dessous quand f(x) < 0.

Comme a = 2 > 0 (ambiance/atmosphère positive : la parabole sourit), la parabole est tournée vers le haut.
Comme Δ > 0, la parabole coupe deux fois l’axe des abscisses.
De plus, la trinôme est du signe de a à l’extérieur des racines.

Voici le tableau de position relative :

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Déterminer la forme canonique de f :

Rédaction :

La forme canonique de f est donnée par cette formule :

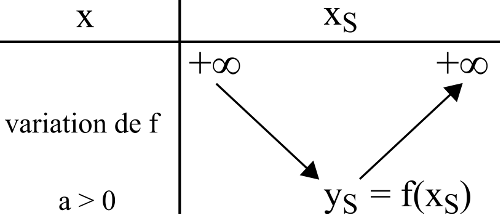
x^S = α = abscisse du sommet
y^S = β = ordonnée du sommet

Ces coordonnées (x^S ; y^S) sont données par :

Ici a = 3, b = -12, c = -15.

x_S = ^-b/_2a = ^-(-12)/_(2×3)
= ¹²/₆ = 2

Δ = b² – 4ac
= (-12)² – 4 × 3 × (-15)
= 144 + 4 × 3 × 15
= 144 + 180
= 324

y_{S = ^-Δ/4a = ^-324/(4×3)
= ^-324/12 = -27}

Donc les coordonnées du sommet S sont (2 ; 27).
On peut aussi calculer y_S avec
f(x_S) = f(2) = 3 × 2² – 12 × 2 – 15
= 12 – 24 – 15
= -27.

Du coup, la forme canonique est :
f(x) = 3(x – 2)² – 27.

2) Déterminer les solutions de l’équation f(x) = 0 :

Rédaction :

f(x) = 0
⇔ 3x² – 12x – 15 = 0

J’ai a = 3, b = -12, c = -15.

Je calcule Δ = b² – 4ac
= (-12)² – 4 × 3 × (-15)
= 144 + 4 × 3 × 15
= 144 + 180
= 324 > 0.

Donc on a deux racines x₁ et x₂ :

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-(-12) – √324)}/_{(2 × 3)}
= ^{(12 – 18)}/₍₆₎
= ^-6/₆
= -1

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-(-12) + √324)}/_{(2 × 3)}
= ^{(12 + 18)}/₍₆₎
= ³⁰/₆
= 5

Donc S = {-1 ; 5}.

3) Coordonnées du point d’intersection de Cf et de l’axe des ordonnées :

Rédaction :

Si Cf coupe l’axe des ordonnées (ce qui donnera ce point d’intersection), c’est que l’abscisse x est égal à 0 car l’axe des ordonnées a pour équation x = 0.
Pour le calcul de l’ordonnée, je rassemble y = f(x) et x = 0, cela fait y = f(0).
y = f(0) = 3 × 0² – 12 × 0 – 15
= – 15.
Le point d’intersection a pour coordonnées (0 ; – 15).

4) Dresser le tableau de variation de f puis allure de Cf :

Rédaction :

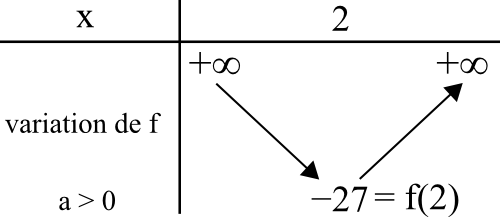
Comme on a les coordonnées du sommet, on sait où s’arrêtent les flèches.
Regardons le signe de « a ». C’est 3 donc il est positif.

(Hors-rédaction : l’atmosphère/ambiance est positive, la parabole sourit.)

Pour notre fonction ici présente :

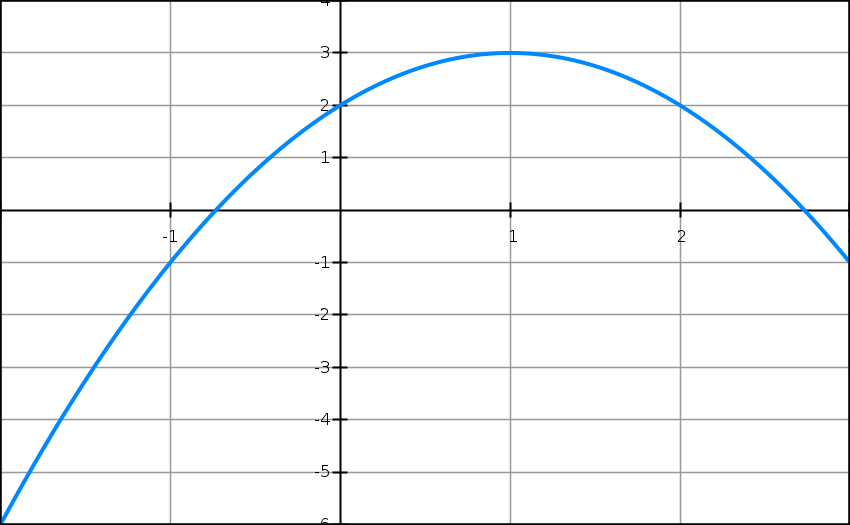
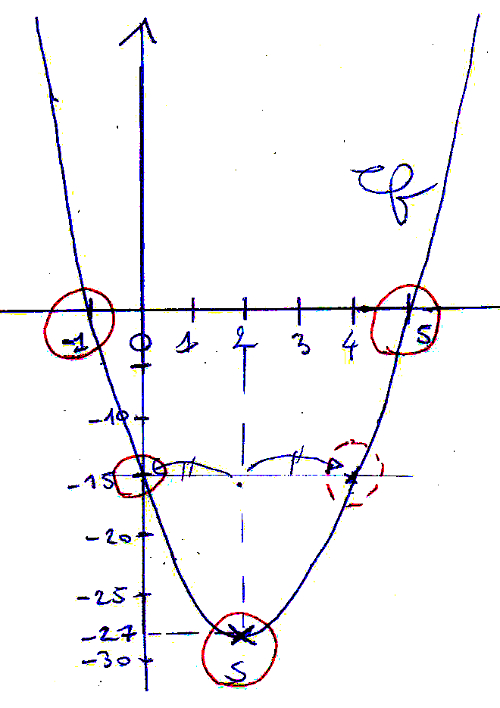
Voici l’allure de la courbe en reprenant les deux points d’intersection avec l’axe des abscisses (abscisses solutions de l’équation f(x) = 0), le point d’intersection avec l’axe des ordonnées, le sommet, et un point symétrique à droite.

PS : je n’ai pas pris le repère donné.

5) Pour chacune de ces fonctions, indiquer laquelle des paraboles la représente :

Rédaction :

Chacune des quatre paraboles a un sommet différent, calculons les abscisses de ces sommets avec les expressions et la formule ^-b/_2a.

g :
x_S = ^-b/_2a = ^-1/_(-2×¹/2)
= ^-1/_(-²/2)
= ⁺¹/₍₊₁₎
= 1
Ce qui correspond à l’abscisse du sommet de C3.

h :
x_S = ^-b/_2a = ^-(-2)/_(2ײ/4)
= ²/_(²/4)
= ²/_(¹/2)
= 2 × ²/₁
= 4
Ce qui correspond à l’abscisse du sommet de C1.

k :
x_S = ^-b/_2a = ^-(-2)/_(-2×¹/3)
= ²/_(-²/3)
= 2 × –³/₂
= -3
Ce qui correspond à l’abscisse du sommet de C2.

l :
x_S = ^-b/_2a = ^-1/_(2×¹/4)
= ^-1/_(²/4)
= ^-1/_(¹/2)
= -1 × ²/₁
= -2
Ce qui correspond à l’abscisse du sommet de C4.

Je récapitule :
(g ; C3) (h ; C1) (k ; C2) (l ; C4)

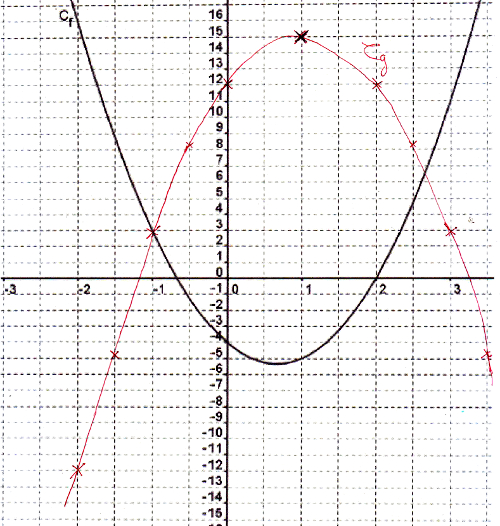
6) Résoudre graphiquement l’inéquation g(x) > h(x) :

Rédaction :

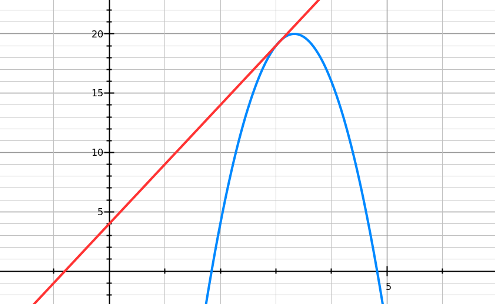
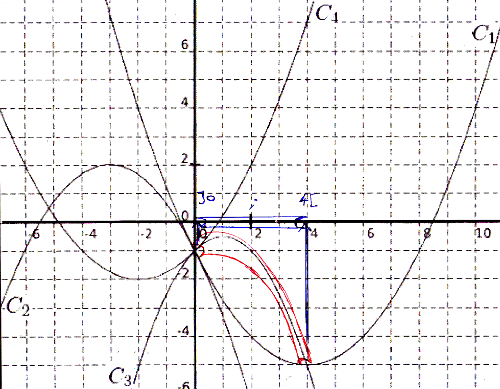
Pour résoudre graphiquement g(x) > h(x), je dois regarder quand la courbe Cg est strictement au dessus de celle de Ch.
C’est à dire quand C3 est au strictement au dessus de C1.
J’entoure les portions de courbe, je descends au niveau des abscisses.

Cela arrive pour les valeurs de x entre 0 et 4.
Donc S = ]0 ; 4[, j’exclus les valeurs 0 et 4 car l’inégalité est stricte.

7) Résoudre les équations suivantes :

4x² – 9 = 0

⇔ (2x)² – 3² = 0 (de la forme a² – b²)
⇔ [(2x) – 3][(2x) + 3] = 0 (en factorisant avec (a-b)(a+b))
Un produit de facteurs est nul si au moins l’un des facteurs est nul.
⇔ (2x – 3) = 0 ou (2x + 3) = 0
⇔ 2x = 3 ou 2x = -3
⇔ x = 3/2 ou x = -3/2
S = {-3/2 ; 3/2}

2x² – 7x = 0

⇔ 2x × x – 7 × x = 0 (de la forme A×K – B#x000d7; K)
⇔ x × (2x – 7) = 0 (de la forme K #x000d7; (A – B))
Un produit de facteurs est nul si au moins de ses facteurs est nul.
⇔ x = 0 ou 2x – 7 = 0
⇔ x = 0 ou 2x = 7
⇔ x = 0 ou x = 7/2
S = {0 ; 7/2}

2004x² + x – 2005 = 0

Impossible de factoriser ici.
Δ = b² – 4ac
= 1² – 4 × 2004 × (-2005)
= 1 + 4 × 3 × 15
= 1 + 16072080
= 16072081 > 0.

Donc on a deux racines x₁ et x₂ :

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-1 – √16072081)}/_{(2 × 2004)}
= ^{(-1 – √16072081)}/₄₀₀₈

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-1 + √16072081)}/_{(2 × 2004)}
= ^{(-1 + √16072081)}/₄₀₀₈

Donc S = {^{(-1 – √16072081)}/₄₀₀₈ ; ^{(-1 + √16072081)}/₄₀₀₈}.

(-³/₄)x² + 2x – 5 = 0

Impossible de factoriser ici.
Δ = b² – 4ac
= 2² – 4 × (-³/₄) × (-5)
= 4 – 3 × 5 (les 4 s’annulent)
= 4 – 15 = -9 < 0

Donc pas de solution.
^{(3x2 + 10x + 8)}/_{(x + 2)} = 2x + 5

On a des fractions dans cette équation donc on passe tout à gauche.
Déjà, on ne peut pas diviser par 0, donc x+2 est différent de 0, donc -2 est valeur exclue de l’ensemble de définition de l’équation.

⇔ ^{(3x2 + 10x + 8)}/_{(x + 2)} – 2x + 5 = 0
⇔ ^{(3x2 + 10x + 8)}/_{(x + 2)} – ^{((2x + 5)×(x + 2))}/_{(x + 2)} = 0
(en mettant au même dénominateur)
⇔ ^{(3x2 + 10x + 8 – (2x + 5)×(x + 2))}/_{(x + 2)} = 0
(en soustrayant les numérateurs)
⇔ ^{(3x2 + 10x + 8 – [(2x + 5)×(x + 2)])}/_{(x + 2)} = 0
(attention au « moins- » donc je mets des crochets)
⇔ ^{(3x2 + 10x + 8 – [2x × x + 2x × 2 + 5 × x + 5 × 2])}/_{(x + 2)} = 0
⇔ ^{(3x2 + 10x + 8 – [2x2 + 4x + 5x + 10])}/_{(x + 2)} = 0
⇔ ^{(3x2 + 10x + 8 – [2x2 + 4x + 5x + 10])}/_{(x + 2)} = 0
⇔ ^{(3x2 + 10x + 8 – 2x2 – 4x – 5x – 10)}/_{(x + 2)} = 0
⇔ ^{(x2 + x – 2)}/_{(x + 2)} = 0
(Une fraction est nulle si et seulement si le numérateur est nul (mais pas le dénominateur), on peut donc enlever le dénominateur).
⇔ x² + x – 2 = 0 et x différent de -2 d’après le domaine de définition de l’équation (valeur exclue).

Δ = b² – 4ac
= 1² – 4 × 1 × (-2)
= 1 + 8
= 9 > 0

Donc on a deux racines x₁ et x₂ :

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-1 – √9)}/_{(2 × 1)}
= ^{(-1 – 3)}/₍₂₎
= ^(-4)/₍₂₎
= -2

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-1 + √9)}/_{(2 × 2004)}
= ^{(-1 + 3)}/₍₂₎
= ⁽²⁾/₍₂₎
= 1

La valeur -2 est exclue car elle n’est pas dans le domaine de définition de cette équation donc S = { 1 }.

Bonne compréhension,
Sylvain Jeuland