Exercice de maths de terminale sur la géométrie dans l’espace : section d’un tétraèdre. Volume, plan, droites, faces, points, pyramide.
Exercice N°225 :
SABCD est une pyramide et ABCD un parallélogramme.
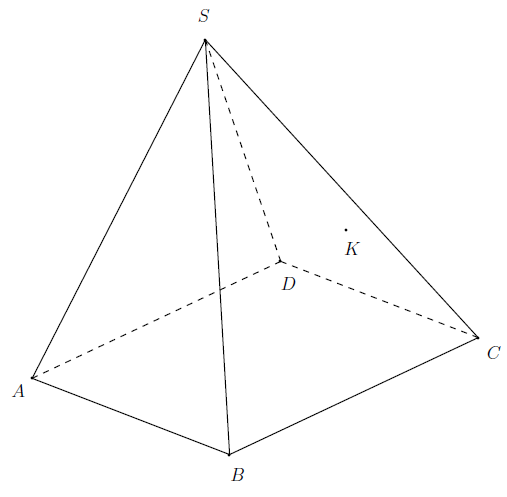
I est le milieu de l’arête [AS], J est le point de l’arête [SB] tel que
SJ = (1/4)SB
et K est un point de la face SDC de la pyramide.
Notre but est de construire la section du tétraèdre par le plan (IJK).
1) Démontrer que l’intersection des plans (SAB) et (SDC) est la droite Δ passant par S et parallèle à (AB).
La droite (IJ) coupe Δ en O.
2) Justifier pourquoi O est un point des plans (IJK) et (SDC).
3) En déduire l’intersection du plan (IJK) avec la face (SDC).
4) Terminer la construction de la section.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : géométrie, espace, section, tétraèdre.
Exercice précédent : Géométrie 3D – Section, cube, pyramide, plan – Terminale

