Maths de première : exercice avec inéquation, second degré. fonctions, coordonnées du sommet, variation, inéquation, courbes, repère.
Exercice N°374 :
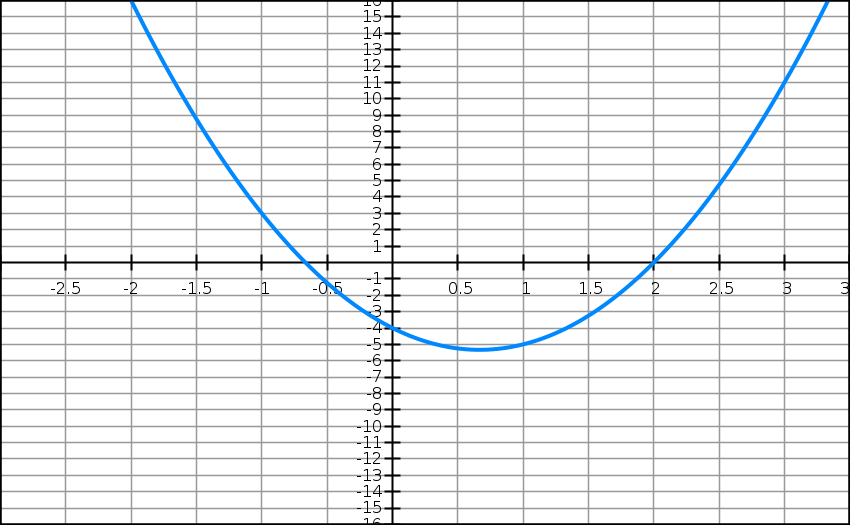
On considère les fonctions f et g définies sur R par
f(x) = 3x2 – 4x – 4
et
g(x) = -3x2 + 6x + 12,
et on note Cf et Cg les représentations graphiques de ces deux fonctions dans un repère orthogonal.
Cf est donnée dans ce repère ci-dessus.
1) Déterminer les coordonnées du sommet de la parabole Cg.
2) Dresser le tableau de variation de g puis tracer Cg dans le même repère que Cf.
3) Résoudre par le calcul l’inéquation
3x2 – 4x – 4 > -3x2 + 6x + 12.
4) Comment peut-on contrôler graphiquement l’ensemble de solution obtenu dans la question précédente ?
Question indépendante :
ABCD est un carré de côté 8 cm et M est un point du segment [AB].
On partage alors le carré en quatre rectangles comme l’indique la figure,
et on note Ag l’aire du domaine coloré en gris sur la figure ci-dessous.
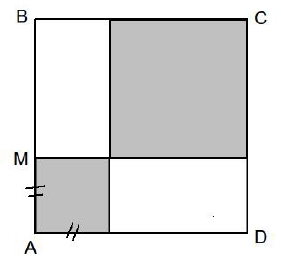
5) J’affirme qu’il existe une seule position de M pour laquelle l’aire Ag est égale à la moitié de l’aire du carré ABCD. Est-ce vrai ?
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, inéquation, second degré.
Exercice précédent : Statistiques – Quartiles, diagramme en boîte, écart – Première

