Essaie les exercices de DS, clique ci-dessous
Maths de première : exercice de suite arithmétique avec somme. Calculs de premiers termes, raison, formule explicite, équations.
Exercice N°111 :
Exercice N°111 :
Soit V la suite définie par V0 = 2 et pour tout entier naturel n,
Vn+1 = 3/(Vn + 1).
1) Calculer V1, V2 et V3. Lis la suite »
Maths de seconde : exercice de fonction avec tableau de variation. Image, antécédent, minimum, maximum, inégalités, encadrement, inégalités.
Exercice N°202 :
Exercice N°202 :
On définit la fonction f par son tableau de variation ci-dessous.
1) Quel est l’ensemble de définition D de la fonction f ? Lis la suite »
Exercice de maths de suite : somme géométrique, arithmétique de première. Sens de variation, calculs de raison, premier terme.
Exercice N°006 :
Exercice N°006 :
1) Étudier le sens de variation de la suite (un) définie par
u0 = 3,
un+1 = 2 un² + un + 3 pour tout n ∈ N. Lis la suite »
Maths de seconde : exercice sur les ensembles de nombres, entiers, relatifs, rationnels, réels, décimaux. Calculs avec fractions et racines.
Exercice N°632 :
Exercice N°632 :
1-2-3-4-5-6-7) Pour chacun des nombres suivants, préciser en justifiant, parmi les ensembles N, Z, D, Q et R le plus petit ensemble (au sens de l’inclusion) auquel il appartient :
1) 2.7, Lis la suite »
Maths : exercice sur l’écart-type de seconde. Statistiques avec moyenne, variance, médiane, quartiles, écart interquartile, proportion.
Exercice N°752 :
Exercice N°752 :
L’entreprise Sheddi vend des roulement à billes. On contrôle le fonctionnement d’une machine qui fabrique des rondelles en aluminium. Sylvain contrôle le fonction d’une machine qui fabrique des rondelles en acier d’un diamètre de 15 mm en théorie, en prélevant de manière aléatoire un échantillon de 120 rondelles dans la fabrication de cette machine.
Les mesures faites sur la machine ont donné les résultats ci-dessous.
1) Calculer la fréquence en pourcentage des rondelles en aluminium ayant un diamètre de 14,8. Lis la suite »
Maths : exercice d’exponentielle avec tangente de première. Dérivées, tableau de variation, inconnues, système d’équations, graphique.
Exercice N°751 :
Dans le plan muni d’un repère orthogonal, la courbe C ci-dessous représente une fonction f définie sur R.
La tangente D à la courbe C au point A(0 ; -4) passe par le point
B(2 ; -6).
1) Donner la valeur de f(0). Lis la suite »
Maths de terminale : exercice d’exponentielle avec continuité et équation. Tableau de variation, solution unique, encadrement.
Exercice N°750 :
Exercice N°750 :
On considère la fonction f définie sur R par
f(x) = (-4x2 + 5)e-x + 3.
On note (C) la courbe représentative de la fonction f dans un repère orthogonal.
On note f ‘ la dérivée de f sur R.
1) Démontrer que pour tout réel x ∈ R,
f ‘ (x) = (4x2 – 8x – 5)e-x. Lis la suite »
Maths de terminale : exercice d’exponentielle avec variation et continuité, équation avec solution unique, coût de production, primitive.
Exercice N°749 :
Exercice N°749 :
Soit f la fonction définie sur [0 ; 5] par
f(x) = (ax + b)e−x
où a et b sont deux réels.
On note f ‘ la fonction dérivée de f.
1) Montrer que pour tout nombre réel x,
f ‘ (x) = (a − b − ax)e−x. Lis la suite »
Maths : exercice d’exponentielle avec bénéfice de première. Dérivée, variation, maximum, quantité, production, inéquation, nombre dérivé..
Exercice N°748 :
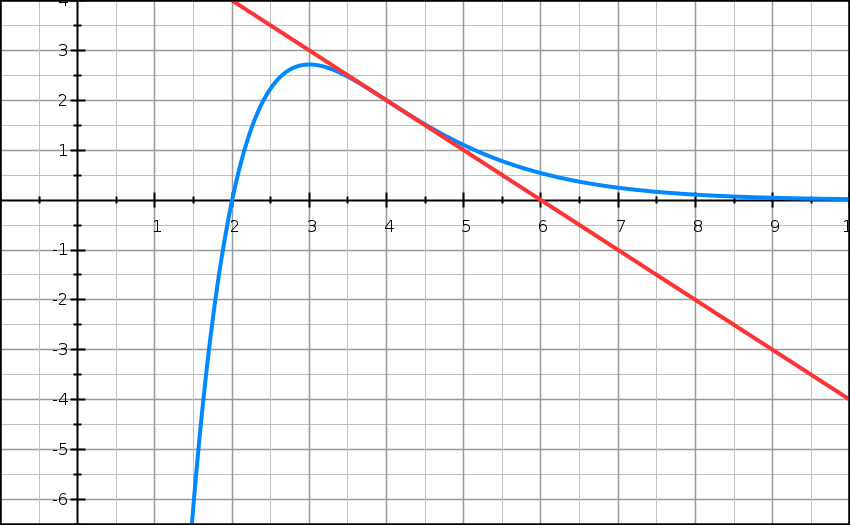
La courbe (C) donnée ci-dessous est la représentation graphique dans un repère orthogonal d’une fonction f définie et dérivable sur [2 ; 9]. On note f ‘ sa fonction dérivée.
Les points A(3 ; e) et B(4 ; 2) appartiennent à cette courbe.
La tangente à la courbe en A est parallèle à l’axe des abscisses et la tangente (T) à la courbe en B coupe l’axe des abscisses au point d’abscisse 6.
1-2) Par lecture graphique, répondre aux deux questions suivantes, sans justifier.
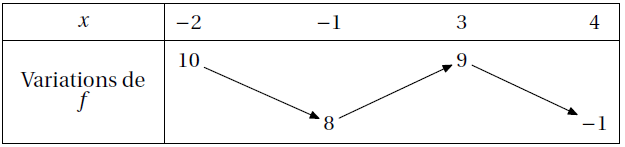
1) Pour quelles valeurs du nombre réel x de l’intervalle [3 ; 9] a-t-on
f(x) ≤ 2 ? Lis la suite »
Maths : exercice de convexité et exponentielle de terminale. Fonctions dérivées, signe, variation, convexe, concave, point d’inflexion.
Exercice N°747 :
On considère la fonction f définie sur R par l’expression :
f(x) = (2x + 1)ex.
1) Étudier le signe de la fonction f. Lis la suite »
