Maths de première : exercice de dérivation avec optimisation de volume. Calcul, surface, tableaux de signe et de variation, maximum.
Exercice N°043 :

Exercice N°043 :
Un vendeur de berlingots veut faire fabriquer une nouvelle boîte de présentation pour Noël. Elle aura la forme d’un prisme droit dont deux des faces sont deux rectangles de 20 cm de longueur sur 5 cm de largeur.
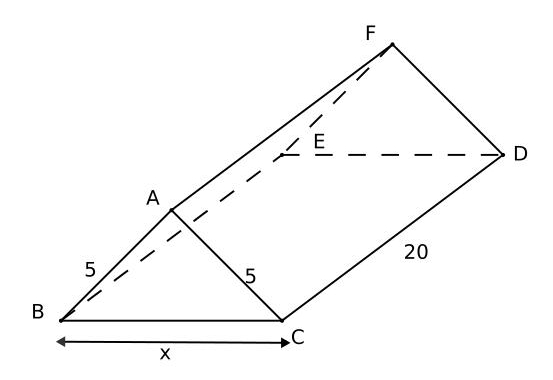
Une section de ce prisme par un plan perpendiculaire à la face BCDE est le triangle ABC isocèle en A. La longueur BC = x représente l’écartement entre les deux rectangles.
Le but du problème est de déterminer x tel que le volume de cette boîte soit le plus grand possible.
1) Quelles sont les valeurs possibles pour x ?
2) Exprimer l’aire du triangle ABC en fonction de x.
3) Exprimer le volume du prisme V en fonction de x.
Soit la fonction f définie sur [0 ; 10] par
f(x) = x2(100-x2).
4) Étudier le sens de variations de f.
5) Pour quelles valeurs de x, f admet-elle un maximum ?
6) Vérifier que
V(x) = 5 × √f(x).
7) En utilisant les variations de f,
déterminer les variations de la fonction V sur [0 ; 10].
8) En déduire les dimensions maximales de la boîte de berlingots ayant le plus grand volume et donner la valeur de ce volume maximal.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, dérivation, optimisation, volume.
Exercice précédent : Dérivation – Fonctions, étude classique d’une fonction – Première


J’ai payé mais je n’ai pas eu le corrigé.
Bonjour,
je viens de vous envoyer le corrigé par courriel. Il suffira d’aller sur les liens.
Bien cordialement, bonne journée,
Sylvain Jeuland