Maths de terminale : exercice, fonction, limite, asymptote, rationnelle, tableau de variation, conjecture, intersection, axe, droite.
Exercice N°250 :
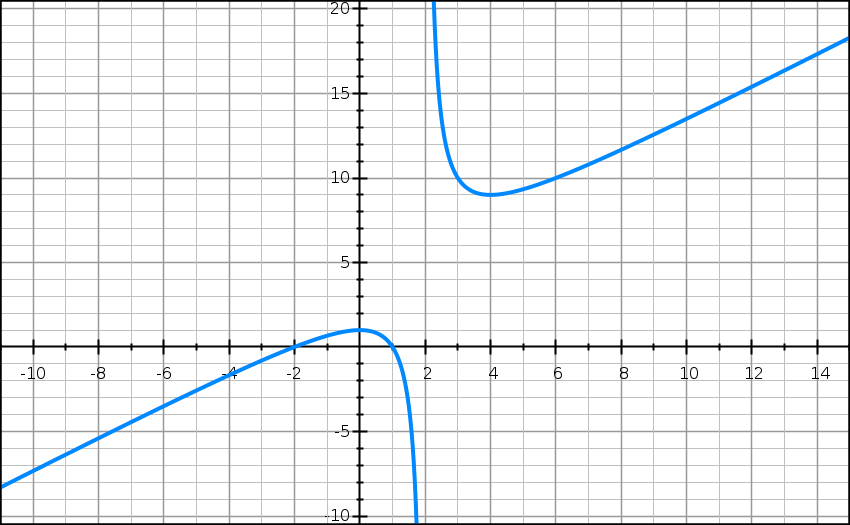
On considère la fonction g définie sur ]-∞ ; 2[ ⋃ ]2 ; +∞[
par
g(x) = (x2 + x – 2)/(x – 2)
et Cg sa courbe représentative dans un repère du plan.
1) Conjecturer, à l’aide du graphique, les variations de la fonction g, et les asymptotes à Cg.
2) Déterminer les réels a, b et c, tels que
g(x)= ax + b + c/(x – 2).
3) Étudier les limites de g aux bornes de son ensemble de définition. Justifier alors certaines conjectures faites en 1).
4) Étudier les variations de la fonction g et dresser son tableau de variation.
5) Déterminer les coordonnées des points d’intersection avec les axes de coordonnées.
Soit (d) la droite d’équation
y = x + 3,
6) La tracer sur le graphique.
Soit M un point de (d) d’abscisse x et F le point sur Cg ayant la même abscisse que M.
7) Montrer que la distance MF tend vers 0 lorsque x tend vers +∞.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, fonction, limite, asymptote.
Exercice précédent : Dérivation – Fonction, dérivabilité, tangente, courbe – Terminale

