Exercice de maths de terminale sur la dérivation avec dérivabilité, interprétation géométrique, tangente, fonction, équation, courbe.
Exercice N°249 :
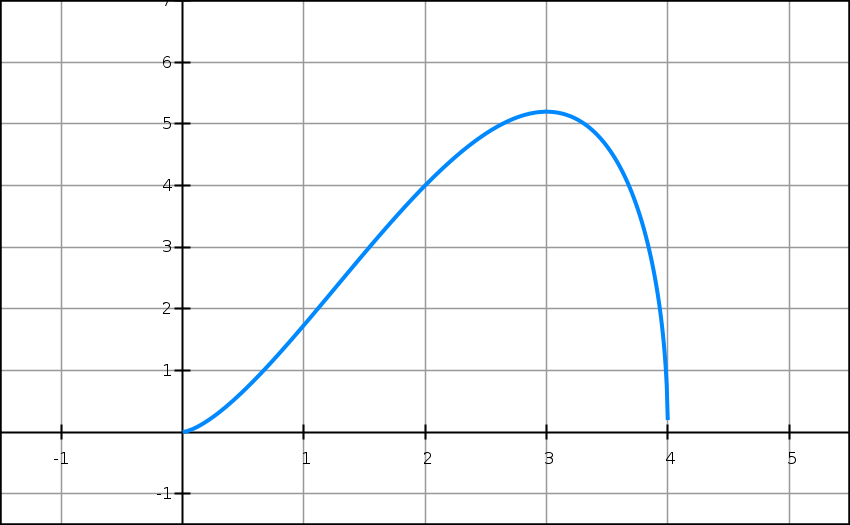
On considère l’expression x√( x × (4−x) ) où x est un nombre réel.
1) Déterminer l’intervalle I = [a ; b] des valeurs pour lesquelles cette expression est calculable.
Soit f la fonction définie sur I par
f(x) = x√( x × (4−x) )
et Cf sa courbe représentative dans un repère du plan.
2) A l’aide des formules de dérivation, calculer f ‘ (x) sur l’intervalle ]0 ; 4[.
3) Étudier la dérivabilité de la fonction f à droite de 0 et à gauche de 4.
En déduire une interprétation géométrique pour Cf.
4) Déterminer l’équation de la tangente à Cf au point d’abscisse 2, puis au point d’abscisse 3.
5) Tracer toutes les tangentes à Cf dont il est question précédemment.
6) Donner le tableau de variation de f.
Autre chose :
7) Calculer la fonction dérivée de la fonction g (on précisera l’ensemble de dérivabilité) :
g(x) = 1/(cos x + 1)4.
8) Calculer la fonction dérivée de la fonction h (on précisera l’ensemble de dérivabilité) :
h(x) = √( (2x + 3)2 + 4 ).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : dérivabilité, interprétation géométrique, tangente.
Exercice précédent : Fonctions – Équations, continuité, variations, limite – Terminale

