Maths de terminale : exercice de fonction, équation, continuité, variation, nombre de solutions, limite en infini, valeurs intermédiaires.
Exercice N°248 :
On considère une fonction f définie sur [0 ; 2π] dont le tableau de variation est donné ci-dessous :
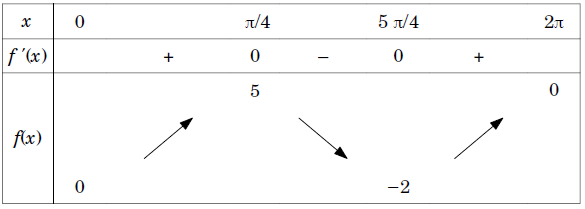
1) Montrer que l’équation f(x) = 1 admet 2 solutions sur [0 ; 2π].
On considère la fonction g définie sur R par :
{ g(x)= 2 − x2 si x ≤ 0,
{ g(x)= sin(2x)/x si x > 0.
2) Démontrer que g est continue sur R.
3) Déterminer le nombre de solutions de l’équation g(x) = 0.
4) Déterminer limx→+∞g(x).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, fonction, équation, continuité.
Exercice précédent : Limites – Calculs, quotients, racines, suites, cosinus – Terminale

