frenchmaths.com (par Sylvain Jeuland)

Exercice de maths avec graphique, tangente, dérivation, première, fonctions, calculs, variations, équations de droites, parallélisme.

Exercice N°059 :

Soit f la fonction définie et dérivable sur [0 ; 8] dont la représentation graphique est la courbe (C) donnée ci-dessous. Les tangentes à cette courbe en certains points sont tracées.

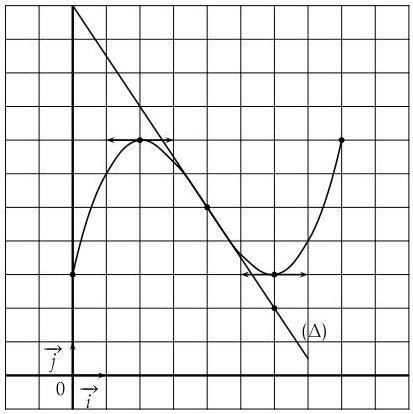
1) Donner par lecture graphique f ‘ (2), f ‘ (4) et f ‘ (6).

2) Donner une équation de la droite Δ.

3) Construire la tangente à la courbe au point d’abscisse 0 sachant que
f ‘ (0) = 7/2.

f est la fonction dérivée de F définie sur [0 ; 8].
4) En justifiant, donner le sens de variations de F.

5-6-7) Calculer dans chaque cas la fonction dérivée :

5) g(x) = x⁴ + ^x3/₅ + 3x² – (⁵/₂)x + 1,

6) h(x) = (3x – 8)(x² – 7x + 1),

7) k(x) = √x(x² + x + 1),

8) l(x) = ¹/_{(2x² – 1)},

9) m(x) = ^{(2x – 3)}/_{(x² + 1)}

Bon courage,
Sylvain Jeuland

Mots-clés de l’exercice : graphique, tangente, dérivation, première.

Exercice précédent : Fonctions – Droite et polynôme du second degré – Première