Exercice sur logarithme népérien avec variation en terminale. Maths, distance, TVI, solution unique, coordonnées, perpendiculaires.
Exercice N°353 :
Exercice N°353 :
Soit u la fonction définie sur ]0 ; +∞[ par :
u(x) = x2 − 2 + ln x.
1) Étudier les variations de u sur ]0 ; +∞[ et préciser ses limites en 0 et en +∞. Lis la suite »
Exercice d’encadrement et intégrale exponentielle. Maths de terminale, primitives, fonction, aire sous la courbe, valeur exacte, signe, unité
Exercice N°477 :
On donne ci-dessus la représentation graphique Cf de la fonction f
définie sur [0 ; 4] par f(x) = (4 − x)e−x.
1) Étudier le signe de f(x) sur [0 ; 4].
On note A l’aire de la zone grise en unités d’aire. Lis la suite »
Maths de terminale : exercice de suite avec récurrence, limite. Arithmétique, géométrique, premier terme, démonstration, égalité.
Exercice N°409 :
Exercice N°409 :
Soit un la suite définie par
{ u0 = 1 ;
{ un+1 = un + 2n + 3.
1) Calculer u1, u2 et u3. Lis la suite »
Maths : exercice avec suite arithmétique de terminale. Fonction, sens de variation, courbe, graphique, convergence, croissance, limite.
Exercice N°410 :
Soit f la fonction définie sur [0 ; 2] par
f(x)= (x − 4)/(x − 3).
1) Étudier les variations de f. En déduire que pour tout x ∈ [0 ; 2],
f(x) ∈ [0 ; 2]. Lis la suite »
Maths de terminale : exercice d’exponentielle, convexité, primitive. Graphique, dérivée, variation, point d’inflexion, position relative.
Exercice N°334 :
Dans le plan muni d’un repère orthogonal, la courbe C ci-dessous représente une fonction f définie sur R.
La tangente D à la courbe C au point A(0 ; -4) passe par le point
B(2 ; -6).
1) Donner la valeur de f(0). Lis la suite »
Exercice de maths de terminale sur la fonction exponentielle, graphique, condition initiale, antécédent, expression, sens de variation.
Exercice N°332 :
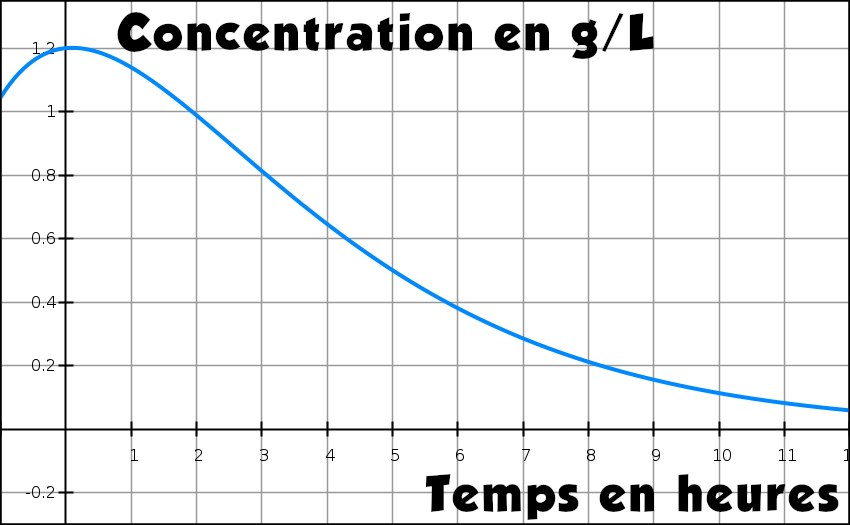
Un groupe de chercheurs étudie l’élimination d’un médicament dans le sang. Pour cela, on a injecté ce médicament par intraveineuse à un patient volontaire, puis on a fait une première mesure à un instant que l’on appelle instant initial : on a trouvé une concentration de 1,2 gramme par litre (g.L-1) dans le sang de ce patient.
A partir de cet instant initial, on a mesuré pendant 24 heures la concentration en gramme par litre de médicament restant dans le sang du patient. Pour les 12 premières heures, on a ainsi obtenu la courbe ci-dessous.
1) Par lecture sur cette courbe, donner la concentration dans le sang au bout de 2 heures ? Lis la suite »
Maths de terminale : exercice de limites sur l’exponentielle avec asymptotes. Dérivées, signe, tableaux de variation, ensemble de définition.
Exercice N°720 :
Exercice N°720 :
Première fonction :
1-2-3-4) La fonction f est définie sur R par
f(x) = (ex – 1)2.
1) Déterminer la limite de f en -∞ en précisant une éventuelle asymptote à la courbe Cf. Lis la suite »
Maths de terminale : exercice de limites sur la fonction exponentielle avec racine, second degré, fractions, plus ou moins l’infini, carré.
Exercice N°719 :
Exercice N°719 :
1-2) La fonction f est définie sur R par
f(x) = (e2x – 3)2.
1) Déterminer la limite de f en +∞ en précisant une éventuelle asymptote à la courbe Cf. Lis la suite »
Maths : exercice de limite d’exponentielle de terminale avec asymptote, calcul de dérivée, tableau de variation, maximum de la fonction.
Exercice N°718 :
Exercice N°718 :
Le nombre d’abonnés à un journal (en milliers) est donné par la fonction f définie sur l’intervalle [0 ; +∞[ par
f(x) = 3e-0.1x² + 0.7x
où x est le temps écoulé (en années) depuis le 1er janvier 2025.
On nomme Cf la courbe représentative de f.
1) Justifier, que pour tout réel x de [0 ; +∞[,
f(x) = 3ex(-0.1x + 0.7). Lis la suite »
Exercice de maths de probabilité sur loi binomiale de terminale avec fluctuation asymptotique. Arbre, espérance, schéma de Bernoulli.
Exercice N°342 :
Exercice N°342 :
Une usine fabrique des balles de tennis qui peuvent avoir deux défauts.
Premier défaut : elles peuvent être mal gonflées, deuxième défaut : elles peuvent être mal formées.
On appelle F l’événement « la balle est bien formée ».
On appelle ¬F l’événement « la balle est mal formée » (¬ signifie « barre »).
On appelle G l’événement « la balle est bien gonflée ».
On sait que P(F) = 0,9 car c’est l’aspect le plus simple à observer (à l’aide d’une caméra).
Si une balle est bien gonflée, elle n’a pas la bonne forme avec une probabilité de 1/23.
Si une balle est mal gonflée, elle est mal formée avec une probabilité de 3/4.
1) Prouver que P(G) = 0,92. Lis la suite »
