Exercice d’encadrement et intégrale exponentielle. Maths de terminale, primitives, fonction, aire sous la courbe, valeur exacte, signe, unité
Exercice N°477 :
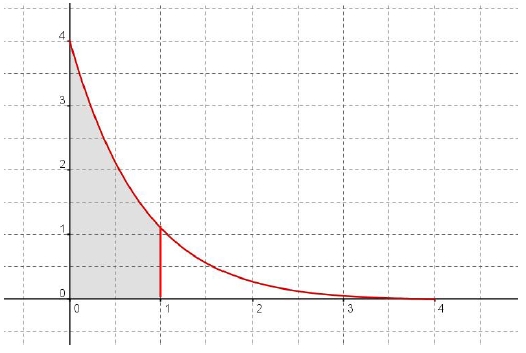
On donne ci-dessus la représentation graphique Cf de la fonction f
définie sur [0 ; 4] par f(x) = (4 − x)e−x.
1) Étudier le signe de f(x) sur [0 ; 4].
On note A l’aire de la zone grise en unités d’aire.
2) Exprimer l’aire A à l’aide d’une intégrale.
3) A l’aide du graphique, donner un encadrement de A d’amplitude inférieure ou égale à 2.
4) Montrer que F définie par F(x) = (x − 3)e−x
est une primitive de f sur [0 ; 4].
5) En déduire la valeur exacte de A puis sa valeur arrondie aux dixièmes.
Autre chose :
6) Déterminer une primitive de la fonction g définie sur R par :
g(x) = (3x – 2)e-3x²+4x.
7) Déterminer toutes les primitives de la fonction h définie sur ]-ln 2 ; +∞[ par :
h(x) = e-2x/(4 – e-2x).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, encadrement, intégrale, exponentielle.
Exercice précédent : Primitives – Exponentielle, convexité, tangente, courbe – Terminale

