Maths de terminale : exercice de primitive, d’intégrale et de convexité, exponentielle, tangente, position relative, courbe, aire, variation.
Exercice N°476 :
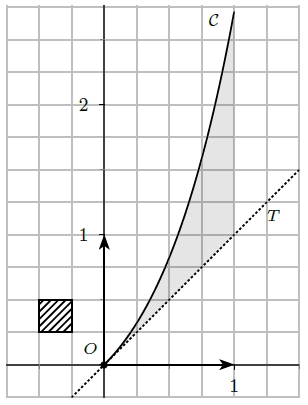
Le plan est muni d’un repère orthonormé (O ; →i ; →j) d’unité graphique 2 cm.
Soit f la fonction définie sur l’intervalle [0 ; 1] par
f(x) = xex.
On note F la primitive de f qui s’annule en x = 1.
On note C la courbe représentative de la fonction f.
Soit b une constante réelle et g la fonction définie sur [0 ; 1] par
g(x) = (x + b)ex.
On répondra par des considérations graphiques pour les quatre premières seulement.
1) Exprimer, en unités d’aires, l’aire du carré hachuré.
2) Expliquer pourquoi on a :
1/8 ≤ ∫[de 0 à 0.5] f(x) dx ≤ 1/4.
3) Expliquer pourquoi F est croissante.
4) Expliquer pourquoi F est convexe.
5) Montrer que pour x ∈ [0 ; 1], on a :
g ‘ (x) = (x + b + 1)ex.
6) Pour quelle valeur de b a-t-on g = f ?
7) Sans recalculer de dérivée, déduire de la question 5) que pour tout x ∈ [0 ; 1] :
f ‘ (x) = (x + 1)ex,
Puis en calculant des dérivées :
f ‘ ‘ (x) = (x + 2)ex,
et
F(x) = (x – 1)ex.
8) Vérifier par le calcul que la tangente T à la courbe C en O a pour équation :
y = x.
9) Étudier la convexité de f. En déduire la position relative de la droite T et de la courbe C.
10) Calculer ∫[de 0 à 1] f(x) dx
11) Calculer l’aire grisée unités d’aires puis en centimètres carrés.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, primitive, intégrale, convexité.
Exercice précédent : Primitives – Graphique, fonction, dérivées, aire – Terminale

