Maths de terminale. Exercice, intégrale, primitive, ln, calculs d’exponentielle, inverse, polynôme du second degré, valeur moyenne.
Exercice N°478 :

Exercice N°478 :
1) Déterminer la primitive F de f définie sur ]0 ; +∞[
par f(x) = 3x2 − (2/x)
s’annulant en x = 1.
2) Calculer ∫[de 1 à 2] 1/(x2) dx.
3) Calculer ∫[de 0 à 1] 4e2x dx.
4) Calculer ∫[de -1 à 3] (x – 3) dx.
5) Calculer ∫[de 1 à 3] (3/(x2)) dx.
6) Calculer ∫[de 0 à 1] 3e-x dx.
7) Montrer que la fonction G définie par l’expression
G(x) = xlnx – x sur ]0 ; +∞[
est une primitive de la fonction
g(x) = ln(x) sur ]0 ; +∞[.
8) Calculer M = ∫[de 1 à 3] ln(x) dx.
La fonction h est définie sur [-1 ; 4] par l’expression :
h(x) = x2 – 2x + 2.
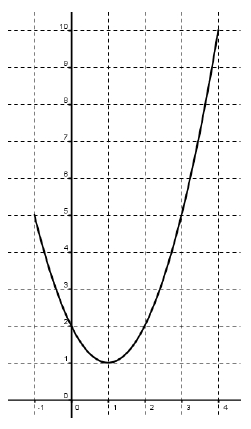
9) Calculer la valeur moyenne de h.
10) Donner une interprétation graphique de cette valeur moyenne. On pourra utiliser le graphique ci-dessus.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, intégrale, primitive, ln.
Exercice précédent : Primitives – Exponentielle, aire, intégrale, encadrer – Terminale

