Maths : exercice de primitive et aire de terminale. Lecture graphique, fonction, dérivée, pente, tangente, surface sous la courbe, signe.
Exercice N°475 :
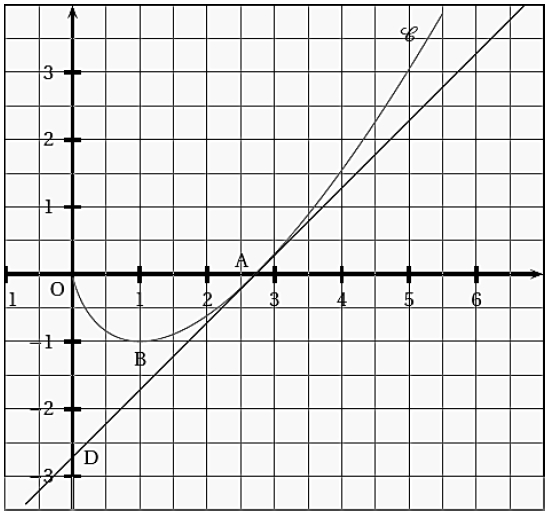
La courbe C ci-dessus représente, dans un repère orthonormé, une fonction f définie et dérivable sur ]0 ; +∞[.
On note f ‘ la fonction dérivée de f. La courbe C passe par les points A(e ; 0) et B(1 ; −1).
La courbe C admet une tangente parallèle à l’axe des abscisses au point d’abscisse 1 et la tangente au point d’abscisse e passe par le point D(0 ; −e).
1) Déterminer une équation de la droite (AD).
Par lectures graphiques :
2) Déterminer f(1) et f ‘ (1).
3) Dresser le tableau de signes de f sur ]0 ; 5].
4) Dresser le tableau de signes de f ‘ sur ]0 ; 5].
Soit F une primitive de f sur ]0 ; +∞[. Déterminer les variations de F sur ]0 ; 5].
5) Encadrer par deux entiers consécutifs l’aire (en unités d’aire) du domaine délimité par l’axe des abscisses, la courbe C
et les droites d’équation x = 4 et x = 5.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, primitive, aire, terminale.
Exercice précédent : Primitives – Fonction, exponentielle, dérivée, TVI – Terminale

