Exercice de maths de terminale sur les primitives, fonction exponentielle, dérivée, intégrale, convexité, point d’inflexion, courbe, TVI.
Exercice N°474 :
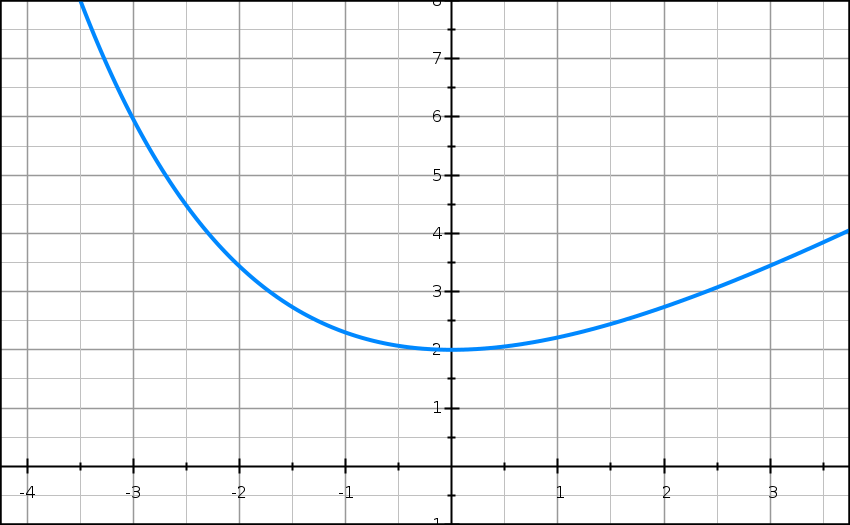
On considère la fonction f définie sur R par
f(x) = 2e−0,5x + x.
On note f la courbe représentative de la fonction f dans le plan muni d’un repère orthogonal (unités graphiques : 2 cm sur l’axe des abscisses et 1 cm sur l’axe des ordonnées).
1) Calculer f ‘ (x).
2) Étudier les variations de f et dresser le tableau de variation de f.
On considère maintenant la fonction F définie sur R par
F(x) = (x2/2) − 4e−0,5x.
3) Montrer que F ‘ (x) = f(x).
4) Étudier les variations de la fonction F.
5) Montrer que l’équation F(x) = 0 a une solution unique a dans R, avec a appartenant à l’intervalle [1 ; 2].
6) Donner une valeur arrondie au dixième près de a.
7) Étudier la convexité de la fonction F.
8) La courbe représentative de de la fonction F a-t-elle un point d’inflexion ?
9) Calculer la valeur exacte de l’intégrale
I = ∫[de -2 à 2] f(x) dx.
10) Hachurer l’aire qui correspond à l’intégrale précédente et donner son aire en UA, puis en cm2.
11) Enfin, tracer la fonction F dans le même repère.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : primitives, fonction exponentielle, dérivée.
Exercice précédent : Primitives – Aires, courbes, intégrales, économie – Terminale

