Maths de terminale : exercice de logarithme népérien avec suite, algorithme. Variation de fonction, construction de termes.
Exercice N°355 :
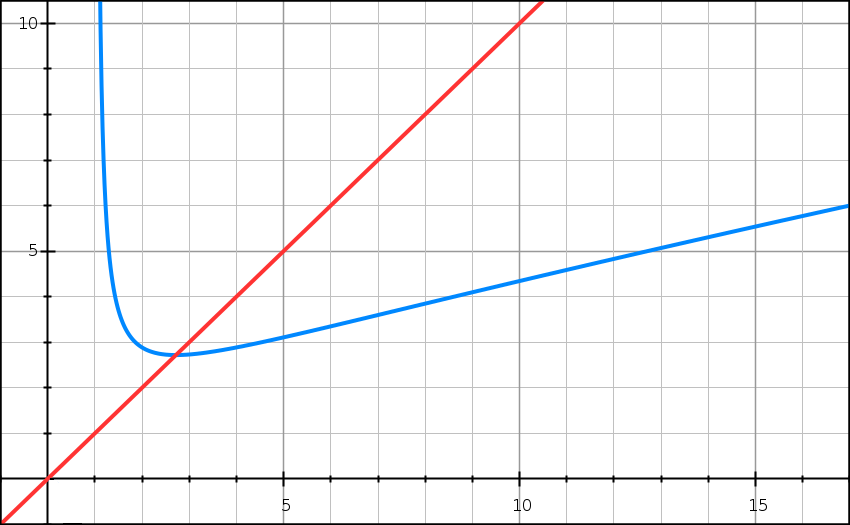
On considère la fonction f définie sur l’intervalle ]1 ; +∞[ par
f(x) = x/(ln x).
Ci-dessus, on a tracé dans un repère orthogonal la courbe C représentative de la fonction f ainsi que la droite D d’équation y = x.
1) Calculer les limites de la fonction f en +∞ et en 1.
2) Étudier les variations de la fonction f sur l’intervalle ]1 ; +∞[.
3) En déduire que si x > e alors f(x) > e.
On considère la suite (un) définie par :
{ u0 = 5,
{ pour tout entier naturel n, un+1 = f(un).
4) Sur le graphique ci-dessus, en utilisant la courbe C et la droite D, placer les points A0, A1 et A2 d’ordonnée nulle et d’abscisses respectives u0, u1 et u2. On laissera apparents les traits de construction.
5) Quelles conjectures peut-on faire sur les variations et la convergence de la suite (un) ?
6) Étudier les variations de la suite (un), et monter qu’elle est minorée par e.
7) En déduire que la suite (un) est convergente.
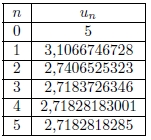
On donne l’algorithme ci-dessous. Par ailleurs, un tableur (en dessous de l’algorithme) donne ces approximations pour certains termes de la suite (un).

8) A l’aide du tableau ci-dessous, déterminer la valeur affichée par l’algorithme.
Un programmeur modifie par erreur l’algorithme en remplaçant la condition
“Tant que X > 2,72”
par
“Tant que X > 2,71”.
9) Commenter cette erreur, si c’en est une.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, logarithme, suite, algorithme.
Exercice précédent : Logarithme Népérien – Équation, exponentielle, fonction – Terminale

