Exercice corrigé sur courbe de Lorenz. Maths de terminale sur les primitives et intégrales avec aire, fonctions affine et polynôme.
Exercice N°473 :
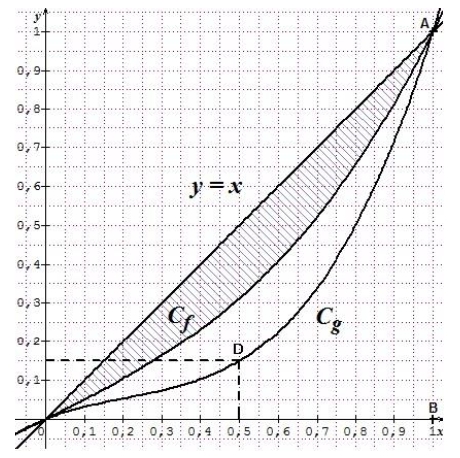
Les deux courbes Cf et Cg représentées ci-dessus illustrent la répartition des richesses dans deux pays 1 et 2. Elles sont définies sur [0 ; 1] et s’appellent
des courbes de Lorentz.
En abscisses, x représente le pourcentage de personnes les plus pauvres par
rapport à la population totale et en ordonnées, y représente le pourcentage de
richesses du pays que ces personnes possèdent.
1) Interpréter économiquement pour le pays 2 les coordonnées du point D de g.
On donne
f(x) = 0.5x3 + 0.5x
et on admet que est positive sur [0 ; 1].
2) Calculer l’aire A1 du domaine délimité par la courbe de f, l’axe des abscisses et les droites d’équations x = 0 et x = 1.
3) En déduire l’aire A du domaine hachuré sur le graphique ci-dessus.
On appelle coefficient de Gini le nombre 2A où A est l’aire du domaine hachuré sur la figure. Le coefficient de Gini évalue le degré d’inégalité de la répartition des richesses. Un coefficient de Gini faible traduit un système égalitaire.
On connaît le coefficient de Gini pour le pays 2 :
G2 = 4/15.
4) Calculer le coefficient de Gini pour le pays 1, noté G1 et en déduire le système le plus égalitaire.
5) Comment pouvait-on prévoir le résultat à l’avance sur le graphique ?
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de Terminale de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice corrigé, courbe de Lorenz.
Exercice précédent : Primitives – Fonction, demande, offre, calculs, moyenne – Terminale

