Exercice de maths sur le calcul d’intégrale et de primitive de terminale. Fonctions de demande et d’offre, point d’équilibre, valeur moyenne.
Exercice N°472 :
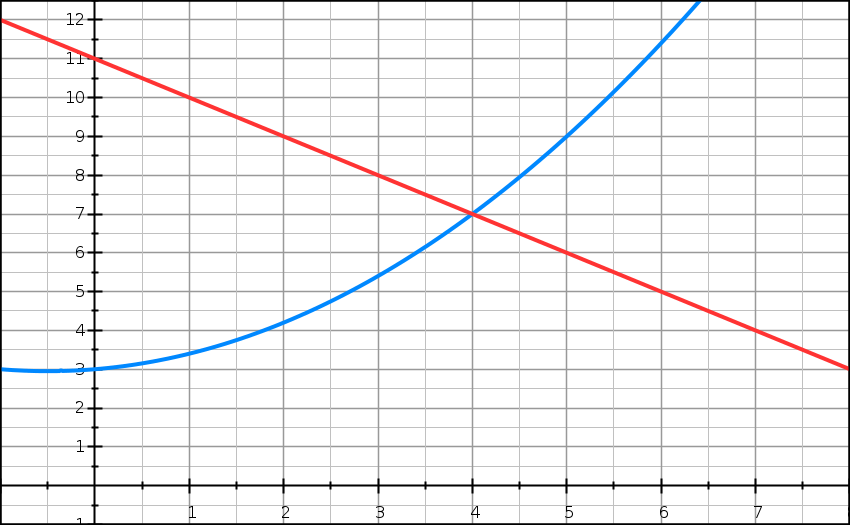
La fonction d’offre d’un bien est définie sur [0 ; 10] par :
f(x) = 0.2x2 + 0,2x + 3 où x est la quantité en tonnes et f(x)
est le prix unitaire en milliers d’euros par tonne.
La fonction de demande de ce bien est définie sur [0 ; 10] par :
g(x) = 11 – x.
Les courbes de f et g sont tracées dans le repère ci-dessus.
1) Résoudre f(x) = g(x) et en déduire la quantité d’équilibre qE, notée et le prix d’équilibre notée pE.
Le surplus des producteurs est défini par :
S = qE × pE – ∫[de 0 à qE] f(x) dx
2) Hachurer en bleu sur le graphique ci-contre l’aire représentée par le surplus (pas de justification).
3) Calculer S (Vous donnerez la valeur exacte et une valeur approchée à 0.01 près).
Soit h la fonction définie sur R par
h(x) = x2 + 2x – 1.
4) Trouver la primitive H de la fonction h qui vérifie :
H(1) = 0.
5) Calculer ∫[de 0 à 2] e2x dx.
6) Calculer la valeur moyenne de la fonction g définie par
k(x) = 4/x2 sur l’intervalle [1 ; 3].
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de Terminale de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : calcul, intégrale, primitive, terminale.
Exercice précédent : Primitives – Rationnelle, signe, intégrale, bénéfice – Terminale

