Exercice de maths de terminale sur primitive et intégrale, fonction rationnelle, étude de signe, aire sous la courbe, bénéfice, moyenne.
Exercice N°471 :
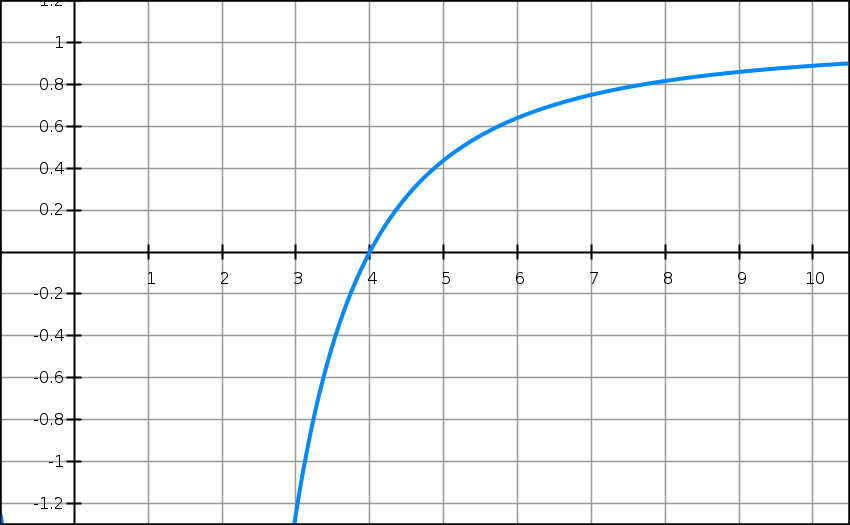
On considère la fonction définie sur [3 ; 10] par
f(x) = (x2 – 2x – 8)/(x – 1)2.
On donne ci-dessus sa courbe Cf dans un repère orthogonal d’unités graphiques : 2 cm en abscisses et 5 cm en ordonnées.
1) Déterminer par calcul le signe de f(x) sur [3 ; 10].
On considère la fonction F définie sur [3 ; 10] par :
F(x)= (x2 + 8)/(x – 1).
2) Montrer que F est une primitive de f sur [3 ; 10].
3) Hachurer et calculer l’aire A du domaine délimité par la courbe Cf, l’axe des
abscisses et les droites d’équations x = 4 et x = 6 (en unités d’aire puis en cm2).
f(x) modélise le bénéfice quotidien (en milliers d’euros) en fonction de la quantité produite x en dizaines d’objets. L’entreprise fabrique entre 30 et 100 objets par jour.
4) A partir de combien d’objets fabriqués le bénéfice est-il positif ? Justifier.
5) Calculer le bénéfice quotidien moyen bm réalisé lorsque l’entreprise produit entre 40 et 60 articles par jour. Placer bm sur le graphique ci-contre et donner une interprétation graphique.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de Terminale de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : primitive, intégrale, fonction rationnelle.
Exercice précédent : Primitives – Intégrales, courbes, dérivée, aire, pente – Terminale

