Exercice de maths de probabilité sur loi binomiale de terminale avec fluctuation asymptotique. Arbre, espérance, schéma de Bernoulli.
Exercice N°342 :

Exercice N°342 :
Une usine fabrique des balles de tennis qui peuvent avoir deux défauts.
Premier défaut : elles peuvent être mal gonflées, deuxième défaut : elles peuvent être mal formées.
On appelle F l’événement “la balle est bien formée”.
On appelle ¬F l’événement “la balle est mal formée” (¬ signifie “barre”).
On appelle G l’événement “la balle est bien gonflée”.
On sait que P(F) = 0,9 car c’est l’aspect le plus simple à observer (à l’aide d’une caméra).
Si une balle est bien gonflée, elle n’a pas la bonne forme avec une probabilité de 1/23.
Si une balle est mal gonflée, elle est mal formée avec une probabilité de 3/4.
1) Prouver que P(G) = 0,92.
2) Montrer que la probabilité qu’une balle prélevée au hasard n’ait aucun défaut est égale à 0,88.
On admet que 88 % des balles produites sont de bonne qualité (elles n’ont aucun défaut). On prélève au hasard 50 balles parmi la production. Le nombre de balles est suffisamment important pour que l’on puisse assimiler ce tirage à un tirage avec remise.
On note X la variable aléatoire qui, à chaque lot de 50 balles tirées, associe le nombre de balles sans défaut.
3) Justifier que X suit une loi binomiale dont on précisera les paramètres.
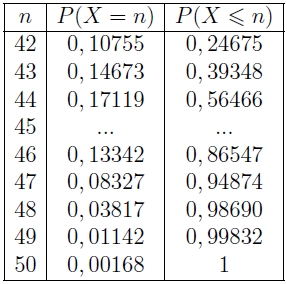
4) Déterminer à l’aide de la calculatrice
P(X = 45) et P(X ≤ 45) à 10−3 près.
5) En utilisant le tableau, calculer la probabilité de tirer un lot contenant au moins 47 balles de bonne qualité.
Après quelques temps d’utilisation des machines, on s’interroge pour savoir si la proportion de balles de bonne qualité est toujours 88 %. On teste alors 1000 balles et on en trouve 855 de bonne qualité.
6) En utilisant un intervalle de “fluctuation asymptotique au seuil de 95 %“, peut-on rejeter l’hypothèse que la proportion de balles de bonne qualité est toujours égale à 88 % ?
7) Calculer l’espérance E(X) de la variable aléatoire X et son écart-type σ(X), arrondir au millième.
On définit la variable aléatoire Y par Y = (X − E(X))/σ(X).
8) En rappelant les formules adéquates, justifier que
E(Y) = 0 et σ(Y) = 1.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : loi binomiale, terminale, fluctuation.
Exercice précédent : Exponentielle – Fonction, dérivée, factorisation – Terminale

