Maths : exercice avec suite arithmétique de terminale. Fonction, sens de variation, courbe, graphique, convergence, croissance, limite.
Exercice N°410 :
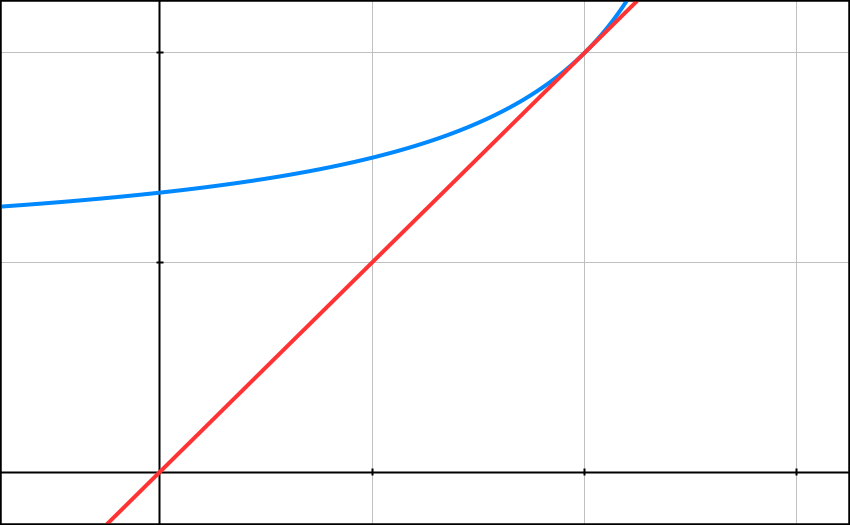
Soit f la fonction définie sur [0 ; 2] par
f(x)= (x − 4)/(x − 3).
1) Étudier les variations de f. En déduire que pour tout x ∈ [0 ; 2],
f(x) ∈ [0 ; 2].
Soit (un) la suite définie par :
{ u0 = 0,
{ un+1 = f(un).
Sur le graphique ci-haut, on a représenté la courbe de f et la droite d’équation
y = x.
2) Placer u0 en abscisse, puis construire u1, u2 et u3 en laissant apparents les traits de construction.
3) Quelle conjecture peut-on faire sur le sens de variation et la convergence de la suite (un) ?
4) Démontrer par récurrence que pour tout n ∈ N,
un ∈ [0 ; 2].
5) Démontrer que (un) est croissante.
6) Démontrer que (un) est convergente.
On pose pour tout n ∈ N :
vn = 1/(un − 2).
7) Démontrer que (vn) est une suite arithmétique de raison −1.
8) Exprimer vn en fonction de n, puis un en fonction de n.
9) En déduire lim n→+∞ un.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, suite, arithmétique, terminale.
Exercice précédent : Suites – Récurrence, arithmétique, géométrique, raison – Terminale

