Maths de terminale : exercice de logarithme népérien et intégrale. Fonction, logarithme, exponentielle, inégalité, variation, asymptote.
Exercice N°460 :
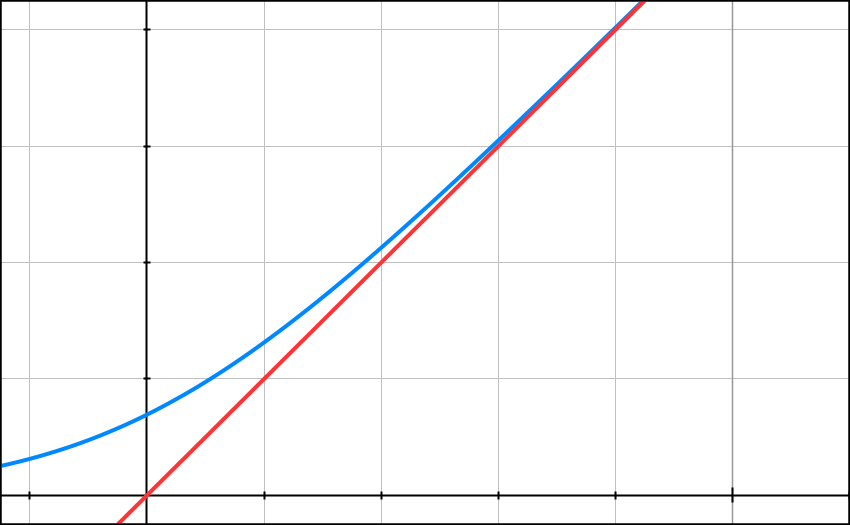
Soit f la fonction définie sur [0 ; +∞[ par :
f(x) = x + ln(1 + e-x).
Sa courbe représentative (C) ainsi que la droite (D) d’équation
y = x
sont données ci-dessous dans un repère orthonormal d’unité graphique 2 cm.
1) Montrer que f est croissante et positive sur [0 ; +∞[. Lis la suite »
Maths de terminale : exercice d’intégrale, logarithme et suite. Fonction, variation, récurrence, fonction, continuité, limite, convergence.
Exercice N°458 :
Exercice N°458 :
On considère la fonction g définie sur l’intervalle [1 ; +∞[ par :
g(x) = ln(2x) + 1 − x.
Cette question demande le développement d’une certaine démarche comportant plusieurs étapes.
1) Démontrer que l’équation g(x) = 0 admet sur l’intervalle [1 ; +∞[ une unique solution notée α.
Donner un encadrement au centième de α.
2) Démontrer que ln(2α) + 1 = α. Lis la suite »
Maths de terminale sur les primitives. Exercice avec encadrement d’une intégrale exponentielle, fonction, limite, intervalles, inégalités.
Exercice N°457 :
Exercice N°457 :
Soit f la fonction définie sur [0; +∞[ par
f(x) = ex/(x + 2).
1) Étudier la limite de la fonction f en +∞. Lis la suite »
Exercice de maths de terminale sur les probabilités avec algorithme, loi uniforme, exponentielle, tableau, loi, fonction de densité.
Exercice N°454 :
On admet que l’on puisse assimiler la fonction « random » d’une calculatrice à une variable aléatoire suivant une loi uniforme sur [0 ; 1].
Soit p un nombre réel appartenant à [0 ; 1].
1) Calculer P(random ≤ p).
On considère l’algorithme ci-dessous :
Maths de terminale : exercice, loi normale, échantillonnage, intervalle de fluctuation, moyenne, écart-type, fréquence, proportion.
Exercice N°453 :
Exercice N°453 :
Une machine fabrique en grande série des pièces d’acier. Soit X la variable aléatoire qui, à toute pièce prise au hasard dans la production hebdomadaire, associe sa longueur, exprimée en cm.
On admet que X suit la loi normale N(15 ; 0,072). Une pièce est déclarée défectueuse si sa longueur est inférieure à 14,9 cm ou supérieure à 15,2 cm.
1) Quelle est la probabilité qu’une pièce prise au hasard dans la production hebdomadaire soit défectueuse ? Lis la suite »
Maths : exercice sur loi exponentielle de terminale, probabilités conditionnelles, sachant, indépendance, binomiale, lambda, intégrale.
Exercice N°452 :
Exercice N°452 :
La durée de vie d’un robot, exprimée en années, jusqu’à ce que survienne la première panne est une variable aléatoire qui suit une loi exponentielle de paramètre λ, avec λ > 0.
Ainsi, la probabilité qu’un robot tombe en panne avant l’instant t est égale à :
p(X ≤ t) = ∫[de 0 à t] λe-λx dx.
1) Déterminer λ, arrondi à 10-1 près, pour que la probabilité p(X > 6) soit égale à 0,3.
Pour la suite de l’exercice, on prendra λ = 0,2. Lis la suite »
Exercice de maths de terminale, probabilité continue avec la loi exponentielle, durée de vie, lambda, intégrale, primitive, intervalle.
Exercice N°450 :
Exercice N°450 :
Une et une seule réponse est exacte pour chaque question.
On s’intéresse à la durée de vie, exprimée en années, d’un appareil ménager avant la première panne. On peut modéliser cette situation par une loi de probabilité p de durée de vie sans vieillissement, définie sur l’intervalle [0 , +∞[. Ainsi, la probabilité d’un intervalle [0 , t[, notée p([0, t[), est la probabilité que l’appareil ménager tombe en panne avant l’instant t.
Cette loi est telle que
p([0 ; t[) = ∫[de 0 à t] λe-λx dx,
où t est un nombre réel positif représentant le nombre d’années (loi exponentielle de paramètre λ, avec λ > 0).
1) Pour t ≥ 0, la valeur exacte de p([t ; +∞[) est :
a) 1 – e-λt, Lis la suite »
Maths de terminale : exercice d’exponentielle avec variation et limite. Fonction, dérivée, TVI, continuité, tableau de signe, solution unique
Exercice N°656 :
Exercice N°656 :
h est la fonction définie sur R par :
h(x) = (3ex – x – 4)e3x.
1) Déterminer la limite de h en -∞. Lis la suite »
Maths de terminale : exercice de probabilités sur loi normale. Réduction, centrée réduite, calculs de surfaces, aires, abscisses, moyenne.
Exercice N°449 :
Exercice N°449 :
On considère une variable aléatoire X qui suit la loi normale N(0 ; 1).
1-5) Déterminer à l’aide de la calculatrice une valeur approchée à 10-3 près des probabilités suivantes :
1) P(0 ≤ X ≤ 1,6), Lis la suite »
Maths de terminale sur les lois de probabilité, exercice, intégrale, normale centrée réduite, formule de, parité, limite, variation..
Exercice N°446 :
Exercice N°446 :
Un peu difficile, à faire en dernier :
La fonction f est définie sur R par :
f(x) = 1/√(2π) × e–x2/2.
Il est rappelé que f est la fonction densité de la loi normale centrée, réduite, d’espérance 0 et d’écart-type 1.
Z est la variable aléatoire associée à N(0, 1).
On rappelle que :
f est paire,
∫[de -∞ à +∞] f(t)dt
= lim[x → -∞] ( ∫[de x à 0] f(t)dt ) + lim[x → +∞] ( ∫[de 0 à x] f(t)dt )
= 1.
Soit G la fonction définie sur [0 ; +∞[ par :
G(x) = ∫[de 0 à x] f(t)dt.
1) Justifier que G admet 1/2 pour limite en +∞.
2) Étudier les variations de G sur [0 ; +∞[. Lis la suite »
